题目内容
10.(2+1)(22+1)(24+1)(28+1)(216+1)+1的计算结果的个位数字是( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
分析 原式变形后,利用平方差公式计算得到结果,归纳总结即可确定出结果的个位数字.
解答 解:原式=(2-1)•(2+1)•(22+1)•(24+1)…(216+1)+1
=(22-1)•(22+1)•(24+1)…(216+1)+1
=(24-1)•(24+1)…(216+1)+1
=232-1+1
=232,
∵21=2,22=4,23=8,24=16,25=32,…,
∴其结果个位数以2,4,8,6循环,
∵32÷4=8,
∴原式计算结果的个位数字为6,
故选:B.
点评 此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
5.方程|x2-4x+3|-k=0有三个实数根,则k的值为( )
| A. | -2 | B. | 2 | C. | 1 | D. | -1 |
2.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.实数a的相反数是( )
| A. | a | B. | -a | C. | $\frac{1}{a}$ | D. | |a| |
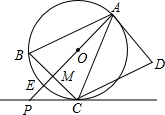 如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.
如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.