题目内容
5.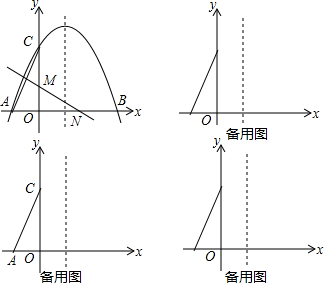 如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.
如图,抛物线y=ax2+bx+4经过点A(-2,0),B(6,0),与y轴交于C.(1)a=-$\frac{1}{3}$,b=$\frac{4}{3}$,抛物线的对称轴是直线x=2,顶点坐标为(2,$\frac{16}{3}$);
(2)M是AC的中点,MN⊥AC交x轴于N,求直线MN的解析式y=kx+b;
(3)点P在抛物线的对称轴上,点Q在x轴上,当四边形ACPQ是轴对称图形时,求点P的纵坐标.
分析 (1)根据待定系数法先求出a、b,再求出对称轴和顶点坐标即可.
(2)根据两条直线垂直k的乘积为-1,利用待定系数法即可解决.
(3)如图①当四边形ACP1Q1是等腰梯形时,CP1=AQ1,AC∥P1Q1,设EQ1=x,由△ACO∽△Q1P1E,得$\frac{AO}{{Q}_{1}E}$=$\frac{CO}{{P}_{1}E}$,列出方程解决问题.
②当四边形ACP2Q2是等腰梯形时,AC=P2Q2,P2C∥AQ2,求出点P纵坐标即可.
解答 解:(1)∵y=ax2+bx+4经过A(-2,0),B(6,0),
∴$\left\{\begin{array}{l}{4a-2b+4=0}\\{36a+6b+4=0}\end{array}\right.$解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴抛物线为y=-$\frac{1}{3}{x}^{2}$+$\frac{4}{3}$x+4.
∴对称轴x=2,顶点(2,$\frac{16}{3}$).
故答案分别为-$\frac{1}{3}$,$\frac{4}{3}$,x=2,(2,$\frac{16}{3}$).
(2)∵M是AC中点,
∴点M坐标(-1,2),
∵直线AC解析式为y=2x+4,AC⊥MN
∴k=-$\frac{1}{2}$,
∴直线MN为y=-$\frac{1}{2}$x+b,把M(-1,2)代入得到b=$\frac{3}{2}$,
∴直线MN解析式为y=-$\frac{1}{2}$x+$\frac{3}{2}$.
(3)如图①当四边形ACP1Q1是等腰梯形时,CP1=AQ1,AC∥P1Q1,设EQ1=x,
∵∠CAO=∠P1Q1E,∠AOC=∠P1EQ1,
∴△ACO∽△Q1P1E,
∴$\frac{AO}{{Q}_{1}E}$=$\frac{CO}{{P}_{1}E}$,
∴$\frac{2}{x}$=$\frac{{P}_{1}E}{4}$,
∴P1E=2x,
∵CP1=AQ1,
∴x+2=$\sqrt{{2}^{2}+(4-x)^{2}}$,解得x=$\frac{7}{5}$,
∴点P纵坐标为$\frac{14}{5}$.
②当四边形ACP2Q2是等腰梯形时,AC=P2Q2,P2C∥AQ2,此时点P纵坐标为4.
综上所述:当四边形ACPQ是轴对称图形时,点P的纵坐标为4或$\frac{7}{5}$.
点评 本题考查抛物线与x轴交点、二次函数的性质、待定系数法,相似三角形的判定和性质等知识,解题的关键是灵活运用这些知识解决问题,学会画图,思考问题要全面,不能漏解,属于中考压轴题.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案| A. | -a2-4b2 | B. | -1+25a2 | C. | $\frac{1}{16}$-9a2 | D. | -a4+1 |
 如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )
如图,正△ABC的边长是2,分别以点B、C为圆心,以r为半径作两条弧,设两弧与边BC围成的阴影部分面积为S,当$\sqrt{2}≤r<2$时,S的取值范围是( )| A. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-$\sqrt{3}$ | B. | $\frac{π}{2}$-1≤S<$\frac{4π}{3}$-1 | C. | 1≤S<$\sqrt{3}$ | D. | $\sqrt{3}≤S$$<2\sqrt{3}$-1 |
 如图:在∠AOB的边OB上有一点C.
如图:在∠AOB的边OB上有一点C.



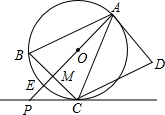 如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.
如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.