题目内容
17.判断下列各式是否正确,如果不正确,举出一个反例来说明(1)$\sqrt{a}$$+\sqrt{b}$=$\sqrt{a+b}$
(2)$\sqrt{a}-\sqrt{b}$=$\sqrt{a-b}$(a>b)
(3)$\sqrt{{a}^{2}-{b}^{2}}$=a-b(a>b)
分析 (1)取a=1,b=4可判断;
(2)取a=9,b=4可判断;
(3)取a=2,b=1可判断.
解答 解:(1)不正确.若a=1,b=4,则$\sqrt{a}$+$\sqrt{b}$=1+2=3,$\sqrt{a+b}$=$\sqrt{5}$;
(2)不正确.若a=9,b=4,则$\sqrt{a}$-$\sqrt{b}$=3-2=1,$\sqrt{a-b}$=$\sqrt{5}$;
(3)不正确.若a=2,b=1,则$\sqrt{{a}^{2}-{b}^{2}}$=$\sqrt{3}$,而a-b=1.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
2.下列各式中,无意义的是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{-2}$ | C. | $\sqrt{(-2)^2}$ | D. | ±$\sqrt{2}$ |
9.下列计算正确的是( )
| A. | $\root{3}{-25}$=-5 | B. | $\root{3}{1\frac{1}{8}}$=1$\frac{1}{2}$ | C. | $\root{3}{125}$=5 | D. | -$\root{3}{-\frac{8}{27}}$=-$\frac{2}{3}$ |
6.下列说法错误的是( )
| A. | -4是16的平方根 | B. | 17是(-17)2的算术平方根 | ||
| C. | $\frac{1}{64}$的算术平方根是$\frac{1}{8}$ | D. | 0.9的算术平方根0.03 |
7.下列各式成立的是( )
| A. | $\sqrt{{a}^{2}}$=a | B. | $\sqrt{(-3)^{2}}$=-3 | C. | $\sqrt{(-3)^{2}}$=±3 | D. | $\sqrt{(-3)^{2}}$=3 |
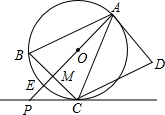 如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.
如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长AO交BC于点M,交$\widehat{BC}$于点E,交过点C的直线于点P,且∠BCP=∠ACD.