题目内容
如图1,在平面直角坐标系中,A(-2,0),C(2,2),过C作CB⊥x轴于B.
(1)如图1,则三角形ABC的面积 ;
(2)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为 ;若AE,DE分别平分∠CAB,∠ODB,求∠AED的度数;
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
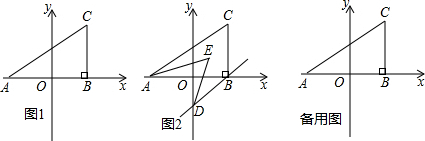
(1)如图1,则三角形ABC的面积
(2)如图2,若过B作BD∥AC交y轴于D,则∠BAC+∠ODB的度数为
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.

考点:坐标与图形性质,三角形的面积,三角形内角和定理,三角形的外角性质
专题:计算题
分析:(1)先利用CB⊥x轴确定C点坐标,然后根据三角形面积公式求解;
(2)连结AD,如图2,根据平行线的性质由BD∥AC得到∠BAC=∠ABD,然后利用∠OBD+∠ODB=90°即可得到∠BAC+∠ODB=90°;根据角平分线定义得∠EAO=
∠BAC,∠EDO=
∠ODB,则可计算出∠EAO+∠EDO=
(∠BAC+∠ODB)=45°,接着根据三角形内角和定理可计算出∠AED=45°.
(3)如图3由OA=OB得到OQ=
BC=1,则Q点坐标为(0,1),设P点坐标为(0,t),根据三角形面积公式得到
•2•|t-1|+
•2•|t-1|=4,然后解绝对值方程得到t的值,从而确定P点坐标.
(2)连结AD,如图2,根据平行线的性质由BD∥AC得到∠BAC=∠ABD,然后利用∠OBD+∠ODB=90°即可得到∠BAC+∠ODB=90°;根据角平分线定义得∠EAO=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)如图3由OA=OB得到OQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵C(2,2),CB⊥x轴于B,
∴C点坐标为(2,0),
∴三角形ABC的面积=
×2×(2+2)=4;
故答案为4;
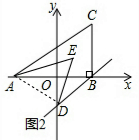
(2)连结AD,如图2,
∵BD∥AC,
∴∠BAC=∠ABD,
∵∠OBD+∠ODB=90°,
∴∠BAC+∠ODB=90°;
∵AE,DE分别平分∠CAB,∠ODB,
∴∠EAO=
∠BAC,∠EDO=
∠ODB,
∴∠EAO+∠EDO=
(∠BAC+∠ODB)=45°,
∵∠AED+∠EAD+∠EDA=180°,即∠AED+∠EA0+∠OAD+∠EDO+∠ODA=180°,
而∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
故答案为90°;
(3)存在.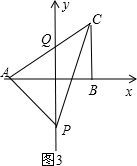
如图3,∵OA=OB,
∴OQ=
BC=1,
∴Q点坐标为(0,1),
设P点坐标为(0,t),
∵三角形ABC和三角形ACP的面积相等,
∴S△PAQ+S△PCQ=4,
即
•2•|t-1|+
•2•|t-1|=4,解得t=3或t=-1,
∴P点坐标为(0,3)或(0,-1).
∴C点坐标为(2,0),
∴三角形ABC的面积=
| 1 |
| 2 |
故答案为4;

(2)连结AD,如图2,
∵BD∥AC,
∴∠BAC=∠ABD,
∵∠OBD+∠ODB=90°,
∴∠BAC+∠ODB=90°;
∵AE,DE分别平分∠CAB,∠ODB,
∴∠EAO=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠EAO+∠EDO=
| 1 |
| 2 |
∵∠AED+∠EAD+∠EDA=180°,即∠AED+∠EA0+∠OAD+∠EDO+∠ODA=180°,
而∠OAD+∠ODA=90°,
∴∠AED+45°+90°=180°,
∴∠AED=45°.
故答案为90°;
(3)存在.

如图3,∵OA=OB,
∴OQ=
| 1 |
| 2 |
∴Q点坐标为(0,1),
设P点坐标为(0,t),
∵三角形ABC和三角形ACP的面积相等,
∴S△PAQ+S△PCQ=4,
即
| 1 |
| 2 |
| 1 |
| 2 |
∴P点坐标为(0,3)或(0,-1).
点评:本题考查了坐标与图形性质:利用点的坐标计算出相应的线段的长和判断线段与坐标轴的位置关系.也考查了三角形内角和定理和三角形外角性质.

练习册系列答案
相关题目
关于x的方程(m+1)xm2+1+4x+2=0是一元二次方程,则m的值为( )
| A、m1=-1,m2=1 |
| B、m=1 |
| C、m=-1 |
| D、无解 |

 如图,已知正六边形ABCDEF的面积为a,AB、CD、EF所在的直线围成△PQR,求△PQR的面积.
如图,已知正六边形ABCDEF的面积为a,AB、CD、EF所在的直线围成△PQR,求△PQR的面积.