题目内容
 如图,已知正六边形ABCDEF的面积为a,AB、CD、EF所在的直线围成△PQR,求△PQR的面积.
如图,已知正六边形ABCDEF的面积为a,AB、CD、EF所在的直线围成△PQR,求△PQR的面积.考点:等边三角形的判定与性质
专题:
分析:连接BE,则四边形AFEB的面积=
a,根据正六边形的性质得出正六边形ABCDEF的各边都相等,每个内角都是120°,进而得出△APF、△BQC、△DRE是等边三角形,然后通过△PAF∽△PBE,求得小三角形的面积,即可求得△PQR的面积.
| 1 |
| 2 |
解答: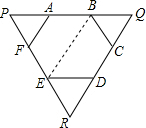 解:连接BE,则四边形AFEB的面积=
解:连接BE,则四边形AFEB的面积=
a,
∵正六边形ABCDEF的各边都相等,每个内角都是120°,
∴△APF、△BQC、△DRE是等边三角形,
∴PF=PA=AB=FE,
∴AF∥BE,
设△APF的面积为S1,
∴
=
,
解得S1=
,
∴△PQR的面积=
×3+a=
a.
 解:连接BE,则四边形AFEB的面积=
解:连接BE,则四边形AFEB的面积=| 1 |
| 2 |
∵正六边形ABCDEF的各边都相等,每个内角都是120°,
∴△APF、△BQC、△DRE是等边三角形,
∴PF=PA=AB=FE,
∴AF∥BE,
设△APF的面积为S1,
∴
| S1 | ||
S1+
|
| 1 |
| 4 |
解得S1=
| a |
| 6 |
∴△PQR的面积=
| a |
| 6 |
| 3 |
| 2 |
点评:本题考查了等边三角形的判定和性质,正六边形的性质,三角形相似的判定和性质,作出辅助线构建相似三角形是本题的关键.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
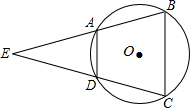 如图,已知⊙O外一点E,过E作两条射线分别交⊙O于A、B、C、D四点,若AE=DE,求证:
如图,已知⊙O外一点E,过E作两条射线分别交⊙O于A、B、C、D四点,若AE=DE,求证:
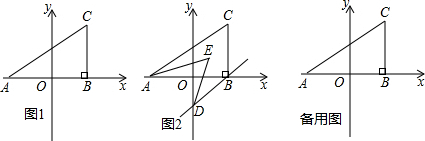
 如图,OM、ON分别是∠BOC和∠AOC的平分线,∠AOB=90°,当OC在∠AOB内转动时,∠MON的值是多少?是否会发生变化?简单说明理由.
如图,OM、ON分别是∠BOC和∠AOC的平分线,∠AOB=90°,当OC在∠AOB内转动时,∠MON的值是多少?是否会发生变化?简单说明理由.