题目内容
关于x的方程（m+1）xm2+1+4x+2=0是一元二次方程，则m的值为（ ）
| A、m1=-1，m2=1 |
| B、m=1 |
| C、m=-1 |
| D、无解 |
考点：一元二次方程的定义
专题：
分析：本题根据一元二次方程的定义求解．
一元二次方程必须满足两个条件：
（1）未知数的最高次数是2；
（2）二次项系数不为0．
由这两个条件得到相应的关系式，再求解即可．
一元二次方程必须满足两个条件：
（1）未知数的最高次数是2；
（2）二次项系数不为0．
由这两个条件得到相应的关系式，再求解即可．
解答：解：由题意得：m2+1=2，m+1≠0，
解得m=±1且m≠-1，
所以m=1，
故选：B．
解得m=±1且m≠-1，
所以m=1，
故选：B．
点评：本题考查了一元二次方程的定义．要特别注意二次项系数a≠0这一条件，当a=0时，上面的方程就不是一元二次方程了，而b，c可以是0．
练习册系列答案
相关题目
下列计算正确的是（ ）
| A、a2+a2=a4 |
| B、（a2）3=a6 |
| C、（3a）•（2a）=6a |
| D、3a-a=3 |
二次函数y=3（x+1）2+2的顶点坐标为（ ）
| A、（-1，-2） |
| B、（-1，2） |
| C、（1，-2） |
| D、（1，2） |
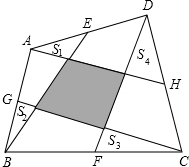如图，E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点，图中阴影部分的面积为20平方厘米，求图中四个小三角形的面积和．