题目内容
9.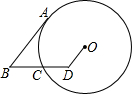 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )| A. | 3+$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{9}{2}$ | D. | $\sqrt{22}$ |
分析 延长CD交⊙O于点E,过点O作OF⊥CE于点F,连接OC,由切割线定理可以求出BE的长度,然后即可求出CE的长度,利用垂径定理即可求出CF的长度,利用勾股定理先求出OF的长度,然后再利用勾股定理即可求出OC的长度,即为半径的长度.
解答 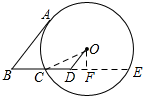 解:延长CD交⊙O于点E,过点O作OF⊥CE于点F,连接OC,
解:延长CD交⊙O于点E,过点O作OF⊥CE于点F,连接OC,
∵BA与⊙O相切,
∴由切割线定理可知:BA2=BC•BE,
∴BE=12,
∴CE=BE-BC=9,
∴由垂径定理可知:CF=$\frac{1}{2}$CE=$\frac{9}{2}$,
∴DF=CF-CD=$\frac{3}{2}$,
∴由勾股定理可知:OF=$\sqrt{O{D}^{2}-D{F}^{2}}$=$\frac{\sqrt{7}}{2}$,
∴由勾股定理可知:OC=$\sqrt{C{F}^{2}+O{F}^{2}}$=$\sqrt{22}$,
故选(D)
点评 本题考查切线的性质,设计切割线定理,勾股定理,垂径定理等知识,综合程度较高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.a4-b4和a2+b2的公因式是( )
| A. | a2-b2 | B. | a-b | C. | a+b | D. | a2+b2 |
4.已知梯形的上、下底分别是1和5,则两腰可以是( )
| A. | 3和8 | B. | 4和8 | C. | 2和2 | D. | 3和5 |
1.若a-b+c=0,则关于x的一元二次方程ax2+bx+c=0必有一根为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
18.下列运算正确的是( )
| A. | (+$\frac{1}{2}$)+(+$\frac{1}{3}$)=$\frac{1}{5}$ | B. | (+$\frac{1}{2}$)+(-$\frac{1}{3}$)=-$\frac{1}{6}$ | C. | (-$\frac{1}{2}$)+(+$\frac{1}{3}$)=$\frac{1}{6}$ | D. | (-$\frac{1}{2}$)+(+$\frac{1}{3}$)=-$\frac{1}{6}$ |
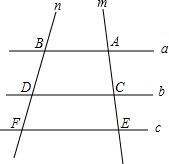 如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:
如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题: