题目内容
20.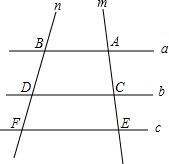 如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:
如图,已知a∥b∥c,n,m分别与a,b,c交于点B,D,F和点A,C,E,试解决下列问题:(1)若AC=6cm,CE=4cm,BD=8cm,求线段DF的长;
(2)若AE:CE=5:2,BD=5cm,求线段DF的长.
分析 (1)由平行线分线段成比例定理得出比例式$\frac{BD}{DF}=\frac{AC}{CE}$,即可求出DF的长;
(2)由比例的性质得出AC:CE=3:2,由平行线分线段成比例定理得出比例式$\frac{BD}{DF}=\frac{AC}{CE}$,即可求出DF的长.
解答 解:(1)∵a∥b∥c,
∴$\frac{BD}{DF}=\frac{AC}{CE}$,
即$\frac{8}{DF}=\frac{6}{4}$,
解得:DF=$\frac{16}{3}$;
(2)∵AE:CE=5:2,
∴AC:CE=3:2,
∵a∥b∥c,
∴$\frac{BD}{DF}=\frac{AC}{CE}$=$\frac{3}{2}$,
即$\frac{5}{DF}=\frac{3}{2}$,
解得:DF=$\frac{10}{3}$.
点评 本题主要考查了平行线分线段成比例定理、比例的性质,掌握平行线分线段可得对应线段成比例是解题的关键.

练习册系列答案
相关题目
11.下列说法正确的是( )
| A. | 每个命题都有逆命题 | B. | 每个定理都有逆定理 | ||
| C. | 所有命题都是定理 | D. | 假命题的逆命题都是假命题 |
9.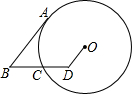 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )| A. | 3+$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{9}{2}$ | D. | $\sqrt{22}$ |
10.某厂一月份到五月份的产值,分别是:350万元,340万元,355万元,400万元,380万元,依据以上数据制作统计图宜选用( )
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 三种都可以 |
 已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.求证:
已知:如图,在平行四边形ABCD中,AB=AD,对角线AC与BD相交于点O.求证: 已知:抛物线y=ax2+2x+c,对称轴为直线x=-1,抛物线与y轴交于点C,与x轴交于A(-3,0)、B两点.
已知:抛物线y=ax2+2x+c,对称轴为直线x=-1,抛物线与y轴交于点C,与x轴交于A(-3,0)、B两点.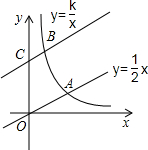 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.