题目内容
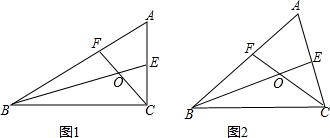
19.△ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.(1)如图1,若∠ACB=90°,求证:BF+CE=BC;
(2)如图2,若∠ABC与∠ACB是任意角度,(1)中的结论是否仍成立?请说明你的理由.
分析 (1)如图1中,在CB上截取CM=CE,连接OM.首先证明△OCE≌△OCM,创造条件证明△OBF≌△OBM即可.
(2)如图2中,在CB上截取CM=CE,连接OM.首先证明△OCE≌△OCM,创造条件证明△OBF≌△OBM即可.
解答 (1)证明:如图1中,在CB上截取CM=CE,连接OM.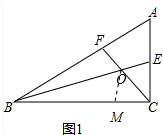
∵∠A=60°,∠ACB=90°,
又∵BE,CF分别是∠ABC和∠ACB的平分线,
∴∠FCA=∠FCB=45°,∠ABE=∠EBC=15°,
∴∠BFC=∠A+∠ACF=105°,∠CEB=∠A+∠ABE=75°
在△OCE和△OCM中,
$\left\{\begin{array}{l}{OC=OC}\\{∠OCM=∠OCE}\\{CE=CM}\end{array}\right.$,
∴△OCE≌△OCM,
∴∠CEO=∠OEC=75°,
∴∠BMO=180°-∠CMO=105°,
∴∠BFO=∠BMO,
在△OBF或△OBM中,
$\left\{\begin{array}{l}{OB=OB}\\{∠OBF=∠OBM}\\{∠BFO=∠BMO}\end{array}\right.$,
∴△OBF≌△OBM,
∴BF=BM,
∴BC=BM+CM=BF+CE.
(2)结论:成立,BC=BF+CE.
理由:如图2中,在CB上截取CM=CE,连接OM.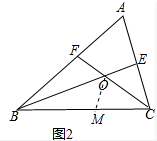
∵∠A=60°,
∴$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=60°,
即∠ABE+∠ACF=60°,
∵∠BFO=∠A+∠FCA,∠CEO=∠A+∠ABE,
∴∠BFO+∠CEO=2∠A+∠FCA+∠ABE=180°,
由△OCM≌△OCE,得∠CEO=∠CMO,
∵∠CMO+∠BMO=180°,
∴∠BFO=∠BMO,
在△OBF或△OBM中,
$\left\{\begin{array}{l}{OB=OB}\\{∠OBF=∠OBM}\\{∠BFO=∠BMO}\end{array}\right.$,
∴△OBF≌△OBM,
∴BF=BM,
∴BC=BM+CM=BF+CE.
点评 本题考查全等三角形的判定和性质、角平分线的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形,这里的难点是角相等的证明,属于中考常考题型.

 名校课堂系列答案
名校课堂系列答案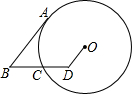 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )| A. | 3+$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{9}{2}$ | D. | $\sqrt{22}$ |
| A. | 扇形图 | B. | 条形图 | C. | 折线图 | D. | 三种都可以 |
(1)两点之间,线段最短;
(2)如果两个角的和是90度,那么这两个角互余.
(3)请画出两条互相平行的直线;
(4)过直线外一点作已知直线的垂线.
| A. | (1)(2) | B. | (3)(4) | C. | (2)(3) | D. | (1)(4) |
| A. |  | B. |  | C. |  | D. |  |
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
| A. | -a2+b2 | B. | -x2-y2 | C. | 49x2y2-z2 | D. | 16m4-25n2 |
 如图,在△ABC中,∠MAC为∠BAC的外角,P为∠MAC的平分线的反向延长线上一点(A除外).
如图,在△ABC中,∠MAC为∠BAC的外角,P为∠MAC的平分线的反向延长线上一点(A除外).