题目内容
17.(1)如图①,在△ABC中,∠A=90°,AB=AC,D是BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,求证:DE=DF.(2)如图②,△ABC是边长为4的等边三角形,D是BC的中点,E、F分别是AB、AC边上的点,且∠EDF=120°,求证:DE=DF.
(3)在(2)的条件下,BE+CF=2(直接写结果)

分析 (1)连接AD,根据等腰直角三角形性质和直角三角形斜边上中线性质求出∠B=∠C=∠BAD=∠DAC=45°,AD=BD,求出∠BDE=∠ADF,根据ASA证△BDE≌△ADF即可;
(2)如图②,连接AD,过D作DM⊥AB交AB于M,再作DN⊥AC交AC于N.根据ASA证明△MDE≌△NDF,再根据全等三角形的性质可得DE=DF;
(3)利用(2)中全等三角形的性质和含30度直角三角形的性质得到BE+CF=$\frac{1}{2}$BC.
解答 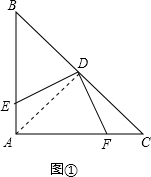 (1)证明:如图①,连接AD.
(1)证明:如图①,连接AD.
∵等腰直角三角形ABC,
∴∠C=∠B=45°,
∵D为BC的中点,
∴AD⊥BC,AD=BD=DC,AD平分∠BAC,
∴∠DAC=∠BAD=45°=∠B,∠ADC=90°,
∵DE⊥DF,
∴∠EDF=90°,
∴∠ADF+∠FDC=90°,∠FDC+∠BDE=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中
$\left\{\begin{array}{l}{∠B=∠DAF}\\{BD=AD}\\{∠BDE=∠ADF}\end{array}\right.$,
∴△BDE≌△ADF,
∴DE=DF.
(2)证明:如图②,连接AD,过D作DM⊥AB交AB于M,再作DN⊥AC交AC于N.
∵△ABC是等边三角形,D为BC的中点,
∴AD是∠BAC的平分线,∠BAC=∠B=∠C=60°
∴DM=DN,∠MDN=120°
又∵∠EDF=120°,
∴∠MDN=∠EDF,
∴∠MDE=∠NDF.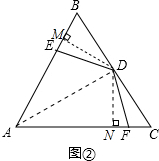
∴在△MDE与△NDF中,$\left\{\begin{array}{l}{∠MDE=∠NDF}\\{DM=DN}\\{∠DME=∠DNF=90°}\end{array}\right.$,
∴△MDE≌△NDF(ASA)
∴DE=DF.
(3)解:如图②,∵由(2)知,△MDE≌△NDF,则ME=NF.
∴BE+CF=BM+EM+CF=BM+NF+CF=BM+CN.
∵在直角△BMD中,∠BDM=30°,
∴BM=$\frac{1}{2}$BD.
同理在直角△DNC中,CN=$\frac{1}{2}$CD.
∴BM+CN=$\frac{1}{2}$(BD+CD)=$\frac{1}{2}$BC.
∵△ABC是边长为4的等边三角形,
∴BC=4,
∴BM+CN=2,即BE+CF=2.
故答案是:2.
点评 本题考查了三角形综合题.需要掌握等腰直角三角形性质,等边三角形的性质,全等三角形的判定与性质以及直角三角形斜边上的中线性质等知识点的应用,关键是①小题构造三角形ADF,证△BDE和△ADF全等,目比较典型,但有点难度.

| A. | $\sqrt{\frac{1}{9}}$ | B. | $\sqrt{18}$ | C. | $\sqrt{8}$ | D. | $\sqrt{12}$ |
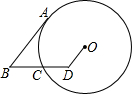 如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )
如图,D为⊙O内一点,BD交⊙O于C,BA切⊙O于A,若AB=6,OD=2,DC=CB=3,则⊙O的半径为( )| A. | 3+$\sqrt{3}$ | B. | 2$\sqrt{6}$ | C. | $\frac{9}{2}$ | D. | $\sqrt{22}$ |
| A. | a=8,b=15,c=17 | B. | a=9,b=12,c=15 | C. | a=7,b=24,c=25 | D. | a=3,b=5,c=7 |
(1)两点之间,线段最短;
(2)如果两个角的和是90度,那么这两个角互余.
(3)请画出两条互相平行的直线;
(4)过直线外一点作已知直线的垂线.
| A. | (1)(2) | B. | (3)(4) | C. | (2)(3) | D. | (1)(4) |
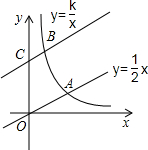 如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.
如图,直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点A,将直线y=$\frac{1}{2}$x向上平移3个单位长度后,与y轴交于点C,与双曲线y=$\frac{k}{x}$(k>0,x>0)交于点B,若OA=3BC,则k的值为$\frac{81}{32}$.