题目内容
4.(1)解不等式组:$\left\{\begin{array}{l}{x+4≥0}\\{2(x-1)+3≥3x}\end{array}\right.$(2)计算:(-π)0-(cos45°)-1-12016+|1-2$\sqrt{\frac{1}{2}}$|
分析 (1)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可;
(2)原式利用零指数幂、负整数指数幂法则,乘方的意义,以及绝对值的代数意义化简,计算即可得到结果.
解答 解:(1)$\left\{\begin{array}{l}{x+4≥0①}\\{2(x-1)+3≥3x②}\end{array}\right.$,
由①得:x≥-4,
由②得:x≤1,
则不等式组的解集为-4≤x≤1;
(2)原式=1-$\sqrt{2}$-1+$\sqrt{2}$-1=-1.
点评 此题考查了解一元一次不等式组,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
19.如果a+b=3,则代数式$\frac{{a}^{2}-{b}^{2}}{a}$÷$\frac{a-b}{2a}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | 3 | D. | 6 |
9.与无理数$\sqrt{33}$-2最接近的整数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
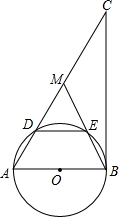 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.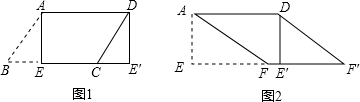

 如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.
如图,已知△ABC.点D,E分别是AB,AC的中点,若△ABC的面积等于24,则△ADE的面积等于6.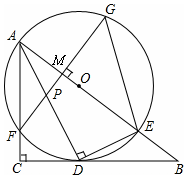 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.