题目内容
14.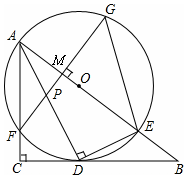 如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.
如图,在Rt△ABC中,∠C=90°,AD是角平分线,DE⊥AD交AB于E,△ADE的外接圆⊙O与边AC相交于点F,过F作AB的垂线交AD于P,交AB于M,交⊙O于G,连接GE.(1)求证:BC是⊙O的切线;
(2)若tan∠G=$\frac{4}{3}$,BE=4,求⊙O的半径;
(3)在(2)的条件下,求AP的长.
分析 (1)连结OD,根据AD是角平分线,求出∠C=90°,得到OD⊥BC,求出BC是⊙O的切线;
(2)构造直角三角形,根据勾股定理求出k的值即可;
(3)设FG与AE的交点为M,连结AG,利用三角函数和相似三角形结合勾股定理解题.
解答 (1)证明:连结OD,
∵DE⊥AD,
∴AE是⊙O的直径,即O在AE上,
∵AD是角平分线,
∴∠1=∠2,
∵OA=OD,
∴∠2=∠3,
∴∠1=∠3,
∴OD∥AC,
∵∠C=90°,
∴OD⊥BC.
∴BC是⊙O的切线;
(2)解:∵OD∥AC,
∴∠4=∠EAF,
∵∠G=∠EAF,
∴∠4=∠G,
∴tan∠4=tan∠G=$\frac{4}{3}$,
设BD=4k,则OD=OE=3k,
在Rt△OBD中,由勾股定理得(3k)2+(4k)2=(3k+4)2,
解得,k1=2,k2=$-\frac{1}{2}$(舍),(注:也可由OB=5k=3k+4得k=2),
∴3k=6,即⊙O的半径为6;
(3)解:连结AG,则∠AGE=90°,∠EGM=∠5.
∴tan∠5=tan∠EGM=$\frac{4}{3}$,
即$\frac{GM}{AM}=\frac{EM}{GM}=\frac{4}{3}$,$\frac{AM}{GM}=\frac{GM}{EM}=\frac{3}{4}$,
∴$\frac{AM}{EM}=\frac{AM}{GM}•\frac{GM}{EM}=\frac{3}{4}×\frac{3}{4}=\frac{9}{16}$,
∴AM=$\frac{9}{25}$AE=$\frac{9}{25}×12$=$\frac{108}{25}$,
∵OD∥AC,
∴$\frac{OD}{AC}=\frac{OB}{AB}$,$\frac{CD}{AO}=\frac{DB}{OB}$,
即$\frac{6}{AC}=\frac{5}{8}$,$\frac{CD}{6}=\frac{8}{10}$.
∴AC=$\frac{48}{5}$,CD=$\frac{24}{5}$,
∵∠1=∠2,∠ACD=∠AMP=90°,
∴△ACD∽△AMP.
∴$\frac{PM}{AM}=\frac{CD}{AC}=\frac{1}{2}$,
∴PM=$\frac{1}{2}AM$=$\frac{54}{25}$.
∴AP=$\sqrt{P{M^2}+A{M^2}}$=$\frac{54}{25}\sqrt{5}$.
点评 本题考查了圆的综合题,涉及切线的判定、勾股定理、相似三角形、特殊角的三角函数值,正确的作出辅助线是解题的关键.

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
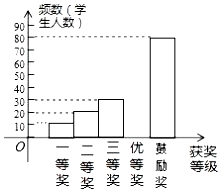 为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:
为了进一步普及足球知识,传播足球文化,某市举行了“足球进校园”知识竞赛活动,为了解足球知识的普及情况,随机抽取了部分获奖情况进行整理,得到下列不完整的统计图表:| 获奖等次 | 频数 | 频率 |
| 一等奖 | 10 | 0.05 |
| 二等奖 | 20 | 0.10 |
| 三等奖 | 30 | b |
| 优胜奖 | a | 0.30 |
| 鼓励奖 | 80 | 0.40 |
(1)a=60,b=0.15;
(2)补全频数分布直方图;
(3)在这次竞赛中,甲、乙、丙、丁四位同学都获得一等奖,若从这四位同学中随机选取两位同学代表该市参加上一级竞赛,请用树状图或列表的方法,计算恰好选中甲、乙二人的概率.
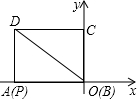 如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),
如图,在平面直角坐标系中,矩形ABCD的边AB,BC分别在x轴,y轴上,点D在第二象限,AB=8,BC=6,矩形ABCD沿OD方向以每秒1个单位长度的速度运动.同时点P从点A出发沿折线AD-DC以每秒1个单位长度向终点C运动,当点P到达点C时,矩形ABCD也停止运动,设点P的运动时间为r(s),△PDo的面积为S(平方单位),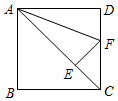 如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.
如图,已知E是正方形ABCD对角线AC上的一点,AE=AD,过点E作AC的垂线,交边CD于点F,∠FAD=22.5度.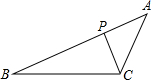 如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).
如图,在△ABC中,P是AB边上的点,请补充一个条件,使△ACP∽△ABC,这个条件可以是:∠ACP=∠B(或$\frac{AP}{AC}$=$\frac{AC}{AB}$)(写出一个即可).