Question

4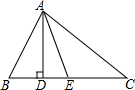．如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=80°，∠C=40°；
（1）求∠BAE的度数；
（2）求∠DAE的度数；
（3）如果只知道∠B-∠C=40°，而不知道∠B∠C的具体度数，你能得出∠DAE的度数吗？如果能求出∠DAE的度数．

Answer 1

分析 （1）根据三角形内角和定理求出∠A，根据角平分线定义求出即可；
（2）求出∠BAD的度数，代入∠DAE=∠BAE-∠BAD求出即可；
（3）根据∠BAE=$\frac{1}{2}$（180°-∠B-∠C）、∠BAD=90°-∠B和已知求出即可．

解答 解：（1）∵∠B=80°，∠C=40°，
∴∠BAC=180°-∠B-∠C=60°，
∵AE平分∠BAC，
∴∠BAE=$\frac{1}{2}$∠BAC=30°；

（2）∵AD⊥BC，
∴∠ADB=90°，
∵∠B=80°，
∴∠BAD=90°-80°=10°，
∴∠DAE=∠BAE-∠BAD=30°-10°=20°；

（3）能求出∠DAE的度数，
理由是：∵由（1）和（2）可知：∠BAE=$\frac{1}{2}$∠A=$\frac{1}{2}$（180°-∠B-∠C），∠BAD=90°-∠B，
∴∠DAE=∠BAE-∠BAD
=$\frac{1}{2}$（90°-∠B-∠C）-（90°-∠B）
=$\frac{1}{2}$∠B-$\frac{1}{2}$∠C，
∵∠B-∠C=40°，
∴∠B=40°+∠C，
∴∠DAE=$\frac{1}{2}$（40°+∠C）-$\frac{1}{2}$∠C=20°．

点评 本题考查了三角形内角和定理，角平分线定义的应用，能求出∠BAE=$\frac{1}{2}$∠A和∠BAD=90°-∠B是解此题的关键．