题目内容
16. 如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是$\sqrt{85}$.
如图是一块长、宽、高分别是6cm、4cm和3cm的长方体木块,一只蚂蚁要从顶点A出发,沿长方体的表面爬到和A相对的顶点B处吃食物,那么它需要爬行的最短路线的长是$\sqrt{85}$.
分析 作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
解答 解:第一种情况:把我们所看到的前面和上面组成一个平面,
则这个长方形的长和宽分别是9和4,
则所走的最短线段是$\sqrt{{4}^{2}+{9}^{2}}=\sqrt{97}$;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是7和6,
所以走的最短线段是$\sqrt{{7}^{2}+{6}^{2}}=\sqrt{85}$;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是10和3,
所以走的最短线段是$\sqrt{{3}^{2}+1{0}^{2}}=\sqrt{109}$;
三种情况比较而言,第二种情况最短.
所以它需要爬行的最短路线的长是$\sqrt{85}$,
故答案为:$\sqrt{85}$
点评 此题考查最短路径问题,解题的关键是明确线段最短这一知识点,然后把立体的长方体放到一个平面内,求出最短的线段.

练习册系列答案
相关题目
7.如果x2-(m-1)x+1是一个完全平方式,则m的值为( )
| A. | -1 | B. | 1 | C. | -1或3 | D. | 1或3 |
11.为了加强公民的节水意识,合理利用水资源,各地采用价格调控手段达到节约用水的目的,某市规定如下用水收费标准:每户每月的用水量不超过6立方米时,水费按每立方米a元收费,超过6立方米时,不超过的部分每立方米仍按a元收费,超过的部分每立方米按c元收费,该市某户今年9、10月份的用水量和所交水费如下表所示:
(1)求a,c的值(列方程组求解);
(2)设某户每月用水量x(立方米),应交水费y(元);分别写出当0≤x≤6,x≥6时,y关于x的函数关系;
(3)若该户11月份用水量为8立方米,求该户11月份水费是多少元?
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
(2)设某户每月用水量x(立方米),应交水费y(元);分别写出当0≤x≤6,x≥6时,y关于x的函数关系;
(3)若该户11月份用水量为8立方米,求该户11月份水费是多少元?
5. 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )| A. | 圆 | B. | 椭圆 | ||
| C. | 一般的平行四边形 | D. | 矩形 |
 如图,已知直线AD,BE相交于点O,∠BOC=90°,OF平分∠AOE,若∠1=35°,求∠2,∠3和∠DOF的度数.
如图,已知直线AD,BE相交于点O,∠BOC=90°,OF平分∠AOE,若∠1=35°,求∠2,∠3和∠DOF的度数.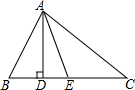 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;