题目内容
13.已知关于x的方程x2-3mx+5m-2=0的一个根为x=2,且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为( )| A. | 8 | B. | 10 | C. | 8或10 | D. | 6或10 |
分析 把x=2代入已知方程求得m的值;然后通过解方程求得该方程的两根,即等腰△ABC的两条边长,由三角形三边关系和三角形的周长公式进行解答即可.
解答 解:把x=2代入方程得4-6m+5m-2=0,
解得m=2,
则原方程为x2-6x+8=0,
解得x1=2,x2=4,
因为这个方程的两个根恰好是等腰△ABC的两条边长,
①当△ABC的腰为4,底边为2,则△ABC的周长为4+4+2=10;
②当△ABC的腰为2,底边为4时,不能构成三角形.
综上所述,该三角形的周长的10.
故选:B.
点评 本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了三角形三边的关系.

练习册系列答案
相关题目
3.已知一角形的两边分别为5和9,则此三角形的第三边可能是( )
| A. | 3 | B. | 4 | C. | 9 | D. | 14 |
5. 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )| A. | 圆 | B. | 椭圆 | ||
| C. | 一般的平行四边形 | D. | 矩形 |
2. 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
 如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )
如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°,则弦BC的长等于( )| A. | $\sqrt{41}$ | B. | $\sqrt{34}$ | C. | 8 | D. | 6 |
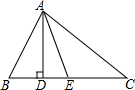 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;
如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80°,∠C=40°;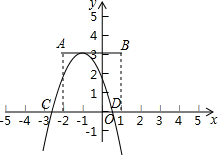 已知点A,B的坐标分别为(-2,3)和(1,3),平移抛物线y=ax2+bx+c(a<0),该抛物线的顶点在线段AB上运动,与x轴交于C、D两点.
已知点A,B的坐标分别为(-2,3)和(1,3),平移抛物线y=ax2+bx+c(a<0),该抛物线的顶点在线段AB上运动,与x轴交于C、D两点.