题目内容
13.将弧长为2πcm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
分析 已知弧长为2πcm,圆心角为120°的扇形,就可以求出扇形的半径,即圆锥的母线长,根据扇形的面积公式可求这个圆锥的侧面积,根据勾股定理可求出圆锥的高.
解答 解:(2π×180)÷120π=3(cm),
2π÷π÷2=1(cm),
$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$(cm),
$\frac{120×π×{3}^{2}}{360}$=3π(cm2).
故这个圆锥的高是2$\sqrt{2}$cm,侧面积是3πcm2.
故选:B.
点评 考查了圆锥的计算,圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
3. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
①BE=$\frac{1}{2}$GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )
 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=$\frac{1}{2}$GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
4. 如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
 如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )
如图,在?ABCD中,O是对角线AC,BD的交点,下列结论错误的是( )| A. | AB∥CD | B. | AB=CD | C. | AC=BD | D. | OA=OC |
18.某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为22元时,该服装店平均每天的销售利润最大.
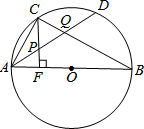 已知,如图Rt△ABC内接于⊙O,AB为直径,CF⊥AB,tan∠ABC=$\frac{3}{4}$,CF=8,D是$\widehat{BC}$的中点,BC与AD的交点为Q,则$\frac{AQ}{DQ}$等于( )
已知,如图Rt△ABC内接于⊙O,AB为直径,CF⊥AB,tan∠ABC=$\frac{3}{4}$,CF=8,D是$\widehat{BC}$的中点,BC与AD的交点为Q,则$\frac{AQ}{DQ}$等于( )