题目内容
6.两条抛物线y1=-$\frac{1}{2}$x2+b,y2=-$\frac{1}{2}$x2-b与分别经过点(-2,0),(2,0)且平行于y轴的两条平行线围成的部分的面积为8,则b等于( )| A. | 1 | B. | -3 | C. | 4 | D. | -1或3 |
分析 根据两函数差的绝对值乘以两条直线的距离=两条抛物线与两条平行线围成部分的面积得:8b=8,可知b=1.
解答 解:∵两解析式的二次项系数相同,
∴两抛物线的形状完全相同,
∴y1-y2=-$\frac{1}{2}$x2+b-(-$\frac{1}{2}$x2-b)=2b;
∴2b×|2-(-2)|=8b=8
∴b=1.
故选:A.
点评 此题主要考查利用二次函数图象的特点求不规则图形的面积,明确两函数差的绝对值乘以两条直线的距离=两条抛物线与两条平行线围成部分的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.在平面直角坐标系中,下列函数的图象经过原点的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-2x-3 | C. | y=2x2+1 | D. | y=5x |
13.将弧长为2πcm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
1.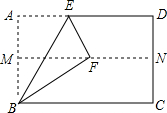 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 36° |
 如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.
如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.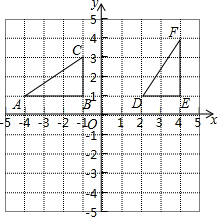 如图,△ABC和△DEF在直角坐标系中的位置如图所示.
如图,△ABC和△DEF在直角坐标系中的位置如图所示.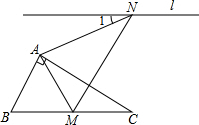 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1的度数为( )
如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1的度数为( )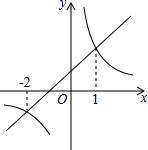 一次函数y1=k1x+b和反比例函数y2=$\frac{{k}_{2}}{x}$(k1k2?≠0)的图象如图所示,若y1>y2,则x的取值范围是-2<x<0或x>1.
一次函数y1=k1x+b和反比例函数y2=$\frac{{k}_{2}}{x}$(k1k2?≠0)的图象如图所示,若y1>y2,则x的取值范围是-2<x<0或x>1.