题目内容
4.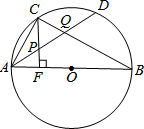 已知,如图Rt△ABC内接于⊙O,AB为直径,CF⊥AB,tan∠ABC=$\frac{3}{4}$,CF=8,D是$\widehat{BC}$的中点,BC与AD的交点为Q,则$\frac{AQ}{DQ}$等于( )
已知,如图Rt△ABC内接于⊙O,AB为直径,CF⊥AB,tan∠ABC=$\frac{3}{4}$,CF=8,D是$\widehat{BC}$的中点,BC与AD的交点为Q,则$\frac{AQ}{DQ}$等于( )| A. | 2.8 | B. | 3 | C. | 3.5 | D. | 4 |
分析 连接OD,根据垂径定理得到OD⊥BC.BE=CE,由圆周角定理得到∠CAD=∠DAB,根据三角函数的定义由tan∠ABC=$\frac{3}{4}$,CF=8,求得BF=$\frac{32}{3}$,BC=$\sqrt{C{F}^{2}+B{F}^{2}}$=$\frac{40}{3}$,AC=10AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{50}{3}$,OD=$\frac{1}{2}$AB=$\frac{25}{3}$,根据三角形的中位线定理得到OE=$\frac{1}{2}$AC=5然后根据△AQC∽△DQE,即可得到结论.
解答  解:连接OD交BC于E,
解:连接OD交BC于E,
∵D是$\widehat{BC}$的中点,
∴OD⊥BC.BE=CE,∠CAD=∠DAB,
∵AB为⊙O直径,
∴∠ACB=90°,
∵CF⊥AB,
∴∠CFB=90°,
∵tan∠ABC=$\frac{3}{4}$,CF=8,
∴BF=$\frac{32}{3}$,
∴BC=$\sqrt{C{F}^{2}+B{F}^{2}}$=$\frac{40}{3}$,
∴AC=10,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\frac{50}{3}$,
∴OD=$\frac{1}{2}$AB=$\frac{25}{3}$,
∵AO=BO,
∴OE=$\frac{1}{2}$AC=5,
∴DE=OD-OE=$\frac{10}{3}$
∵∠ACB=∠DEQ,∠AQC=∠DQE,
∴△AQC∽△DQE,
∴$\frac{AQ}{DQ}=\frac{AC}{DE}$=$\frac{10}{\frac{10}{3}}$=3.
故选B.
点评 本题主要考查相似三角形的判定和性质、勾股定理、圆周角定理、解直角三角形,垂径定理,连接OD构造相似三角形是解题的关键.

| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
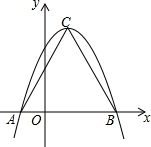 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
| A. | (2,3) | B. | (-2,3) | C. | (2,-3) | D. | (-2,-3) |
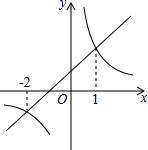 一次函数y1=k1x+b和反比例函数y2=$\frac{{k}_{2}}{x}$(k1k2?≠0)的图象如图所示,若y1>y2,则x的取值范围是-2<x<0或x>1.
一次函数y1=k1x+b和反比例函数y2=$\frac{{k}_{2}}{x}$(k1k2?≠0)的图象如图所示,若y1>y2,则x的取值范围是-2<x<0或x>1.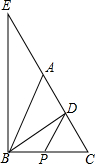 如图,在△ABC中,AB=AC,BD⊥AC于点D,过点B作BE⊥BC交CA的延长线于点E,点P是BC的中点,连接PD,则下列结论:①∠BAC=2∠DBC;②BC2=2CD•AB;③若BC=15,BD=12,则AD=$\frac{7}{2}$;④图中一定相似的三角形有5对,其中正确结论的个数是( )
如图,在△ABC中,AB=AC,BD⊥AC于点D,过点B作BE⊥BC交CA的延长线于点E,点P是BC的中点,连接PD,则下列结论:①∠BAC=2∠DBC;②BC2=2CD•AB;③若BC=15,BD=12,则AD=$\frac{7}{2}$;④图中一定相似的三角形有5对,其中正确结论的个数是( )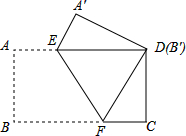 把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重叠,折痕为EF,若DF=3,∠FDC=30°,则△DEF的周长是9.
把一张矩形纸片ABCD按如图方式折叠,使顶点B和顶点D重叠,折痕为EF,若DF=3,∠FDC=30°,则△DEF的周长是9.