题目内容
3. 如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:
如图,G,E分别是正方形ABCD的边AB,BC的点,且AG=CE,AE⊥EF,AE=EF,现有如下结论:①BE=$\frac{1}{2}$GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH
其中,正确的结论有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据正方形的性质得出∠B=∠DCB=90°,AB=BC,求出BG=BE,根据勾股定理得出BE=$\frac{\sqrt{2}}{2}$GE,即可判断①;求出∠GAE+∠AEG=45°,推出∠GAE=∠FEC,根据SAS推出△GAE≌△CEF,即可判断②;求出∠AGE=∠ECF=135°,即可判断③;求出∠FEC<45°,根据相似三角形的判定得出△GBE和△ECH不相似,即可判断④.
解答 解:∵四边形ABCD是正方形,
∴∠B=∠DCB=90°,AB=BC,
∵AG=CE,
∴BG=BE,
由勾股定理得:BE=$\frac{\sqrt{2}}{2}$GE,∴①错误;
∵BG=BE,∠B=90°,
∴∠BGE=∠BEG=45°,
∴∠AGE=135°,
∴∠GAE+∠AEG=45°,
∵AE⊥EF,
∴∠AEF=90°,
∵∠BEG=45°,
∴∠AEG+∠FEC=45°,
∴∠GAE=∠FEC,
在△GAE和△CEF中
$\left\{\begin{array}{l}{AG=CE}\\{∠GAE=∠CEF}\\{AE=EF}\end{array}\right.$
∴△GAE≌△CEF,∴②正确;
∴∠AGE=∠ECF=135°,
∴∠FCD=135°-90°=45°,∴③正确;
∵∠BGE=∠BEG=45°,∠AEG+∠FEC=45°,
∴∠FEC<45°,
∴△GBE和△ECH不相似,∴④错误;
即正确的有2个.
故选B.
点评 本题考查了正方形的性质,等腰三角形的性质,全等三角形的性质和判定,相似三角形的判定,勾股定理等知识点的综合运用,综合比较强,难度较大.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.如图,这是某用户银行存折中2012年11月到2013年5月间代扣电费的相关数据,从中可以看出扣缴电费最多的一次达到( )


| A. | 147.40元 | B. | 143.17元 | C. | 144.23元 | D. | 136.83元 |
13.将弧长为2πcm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
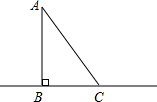 如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)
如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸C的C处测得∠BCA=50°,BC=10m,则桥长AB=11.9m(用计算器计算,结果精确到0.1米)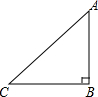 如图所示;△ABC是等腰三角形,∠ABC=90°.
如图所示;△ABC是等腰三角形,∠ABC=90°.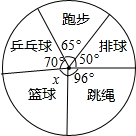 如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数.
如图,这是某校初三年级同学们最喜爱的一项课外运动调查结果扇形图,但负责画此图的同学忘记了最喜爱篮球运动的人数. 如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.
如图,已知圆锥的底面⊙O的直径BC=6,高OA=4,则该圆锥的侧面展开图的面积为15π.