题目内容
1.设y=ax,若代数式(x+y)(x-2y)+3y(x+y)化简的结果为x2,请你求出满足条件的a值.分析 先利用因式分解得到原式(x+y)(x-2y)+3y(x+y)=(x+y)2,再把当y=ax代入得到原式=(a+1)2x2,所以当(a+1)2=1满足条件,然后解关于a的方程即可.
解答 解:原式=(x+y)(x-2y)+3y(x+y)=(x+y)2,
当y=ax,代入原式得(1+a)2x2=x2,
即(1+a)2=1,
解得:a=-2或0.
点评 本题考查了因式分解的运用:利用因式分解解决求值问题;利用因式分解解决证明问题;利用因式分解简化计算问题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
16.在平面直角坐标系中,下列函数的图象经过原点的是( )
| A. | y=$\frac{1}{x}$ | B. | y=-2x-3 | C. | y=2x2+1 | D. | y=5x |
13.将弧长为2πcm,圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高及侧面积分别是( )
| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
12.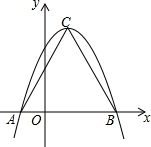 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )
 如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )
如图,二次函数y=-x2+2x+3的图象与x轴交于点A和点B,顶点为C,则sin∠ABC=( )| A. | $\frac{2\sqrt{5}}{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | 2 | D. | $\frac{1}{2}$ |
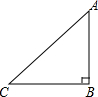 如图所示;△ABC是等腰三角形,∠ABC=90°.
如图所示;△ABC是等腰三角形,∠ABC=90°.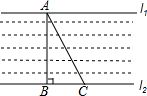 如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)
如图,一条河的两岸l1,l2互相平行,在一次综合实践活动中,小颖去测量这条河的宽度,先在对岸l1上选取一个点A,然后在河岸l2时选择点B,使得AB与河岸垂直,接着沿河岸l2走到点C处,测得BC=60米,∠BCA=62°,请你帮小颖算出河宽AB(结果精确到1米).(参考数据:sin62°≈0.88,cos62°≈0.47,tan62°≈1.88)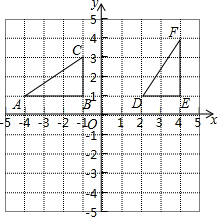 如图,△ABC和△DEF在直角坐标系中的位置如图所示.
如图,△ABC和△DEF在直角坐标系中的位置如图所示.