题目内容
6. 在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.
在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.
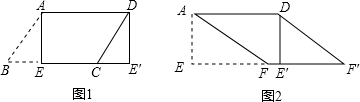
分析 作EF∥BC,CF∥BE,EF与CF相交于F,连接DF,则四边形BEFC为平行四边形,再由四边形ABCD为平行四边形,易证四边形AEFD为平行四边形,得出BE=CF,AE=DF,∠DEF=∠EDA,由SSS证得△ABE≌△DCF,得出∠BAE=∠CDF,∠ABE=∠DCF,证得∠DEF=∠DCF,则E、D、F、C四点共圆,推出∠CDF=∠CEF,即可得出结论.
解答 证明:作EF∥BC,CF∥BE,EF与CF相交于F,连接DF,如图所示:
∵EF∥BC,CF∥BE,
∴四边形BEFC为平行四边形,
∴∠BCE=∠CEF,BC∥EF,BC=EF,
∵四边形ABCD为平行四边形,
∴AB=CD,BC∥AD,BC=AD,
∴EF∥AD,EF=AD,
∴四边形AEFD为平行四边形,
∴BE=CF,AE=DF,∠DEF=∠EDA,
在△ABE和△DCF中,$\left\{\begin{array}{l}{BE=CF}\\{AE=DF}\\{AB=CD}\end{array}\right.$,
∴△ABE≌△DCF(SSS),
∴∠BAE=∠CDF,∠ABE=∠DCF,
∵∠ABE=∠EDA,∠DEF=∠EDA,
∴∠DEF=∠DCF,
∴E、D、F、C四点共圆,
∴∠CDF=∠CEF,
∵∠BCE=∠CEF,∠BAE=∠CDF,
∴∠BAE=∠BCE.
点评 本题主要考查了平行四边形的判定与性质、全等三角形的判定与性质、四点共圆的判定与性质等知识,通过作辅助线构建平行四边形是解决问题的关键.

练习册系列答案
相关题目
8.对于二次函数y=(x+1)2-3,下列说法正确的是( )
| A. | 图象开口方向向下 | B. | 图象与y轴的交点坐标是(0,-3) | ||
| C. | 图象的顶点坐标为(1,-3) | D. | 抛物线在x>-1的部分是上升的 |
17.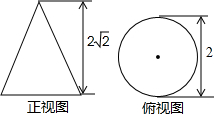 如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
 如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
18.在数学课上,老师提出如下问题:
小云的作法如下:
小云作图的依据是四条边相等的四边形为菱形,菱形的对边平行.
尺规作图:过直线外一点作已知直线的平行线. 已知:直线l及其外一点A. 求作:l的平行线,使它经过点A. |
| (1)在直线l上任取一点B; (2)以B为圆心,BA长为半径作弧,交直线l于点C; 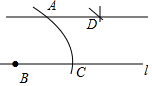 (3)分别以A、C为圆心,BA长为半径作弧,两弧相交于点D; (4)作直线AD. 直线AD即为所求. |
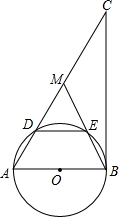 如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.
如图,在Rt△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径做⊙O分别交AC,BM于点D、E.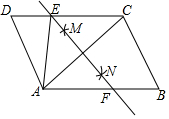 如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为8.
如图,在平行四边形ABCD中,连接AC,按一下步骤作图,分别以点A,点C为圆心,以大于$\frac{1}{2}$AC的长为半径画弧,两弧分别相交于点M、N,作直线MN交CD于点E,交AB于点F,若AB=5,BC=3,则△ADE的周长为8.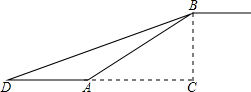 如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).
如图,在合肥地铁3号线某站通道的建设中,建设工人将坡长为20米(AB=20米)、坡角为20°30′(∠BAC=20°30′)的斜坡通道改造成坡角为12°30′(∠BDC=12°30′)的斜坡通道,使斜坡的起点从点A处向左平移至点D处,求改造后的斜坡通道BD的长.(结果精确到0.1米.参考数据:sin12°30′≈0.22,sin20°30′≈0.35,sin69°30′≈0.94).