题目内容
17.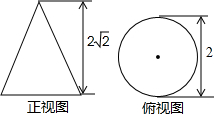 如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )
如图是一圆锥的正视图、俯视图及相关数据,该圆锥的侧面展开图是一个扇形,则该扇形的圆心角的度数是( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
分析 根据圆锥的主视图可以得到圆锥的高和圆锥的底面直径,求出圆锥的底面周长就是侧面展开扇形的弧长,代入公式求得即可.
解答 解:圆锥的主视图可以得到圆锥的高2$\sqrt{2}$和圆锥的底面直径2,
∴圆锥的母线长为$\sqrt{(2\sqrt{2})^{2}+{1}^{2}}$=3,
∴圆锥的底面周长为:πd=2πcm,
∵圆锥的侧面展开扇形的弧长等于圆锥的底面圆的周长,
∴圆锥的侧面展开扇形的弧长为2πcm,
∴圆锥的侧面展开扇形的面积为:$\frac{1}{2}$lr=$\frac{1}{2}$×2π×3=3π,
∴$\frac{nπ×{3}^{2}}{360}$=3π,
解得:n=120.
故选C.
点评 本题考查了圆锥的计算,解题的关键是正确地理解圆锥和侧面扇形的关系.

练习册系列答案
相关题目
19.国家文物局2012年6月5日在北京居庸关长城宣布:中国历代长城总长度为21196.18千米.这是中国首次科学、系统地测量历代长城的总长度.数21196.18保留3个有效数字,用科学记数法表示正确的是( )
| A. | 2.11×104 | B. | 2.12×104 | C. | 0.212×105 | D. | 0.21×105 |
20.若x=1是方程ax2+bx-2=0的一个根,则a+b的值是( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
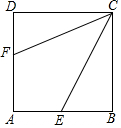 如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.
如图.正方形ABCD的边长为6.点E,F分别在AB,AD上.若CE=$3\sqrt{5}$,且∠ECF=45°,则CF的长为2$\sqrt{10}$.
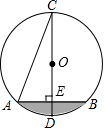 如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为$\frac{9}{2}$π-9,.
如图,在⊙O中,CD是直径,弦AB⊥CD,垂足为E,若∠C=22.5°,AB=6cm,则阴影部分面积为$\frac{9}{2}$π-9,. 在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.
在平行四边形ABCD内取一点,使得∠ABE=∠EDA,求证:∠BAE=∠BCE.