题目内容
抛物线y=x2+bx+c与直线y=x交于A(x1,y1)、B(x2,y2)两点,且满足x1>0,x2-x1>1.
(1)试证明:c>0;
(2)试比较b2与2b+4c的大小;
(3)若c=
,AB=2,试确定抛物线的解析式.
(1)试证明:c>0;
(2)试比较b2与2b+4c的大小;
(3)若c=
| 1 |
| 2 |
考点:二次函数图象与系数的关系
专题:
分析:(1)先将y=x2+bx+c代入y=x,整理得出x2+(b-1)x+c=0,由根与系数的关系得出x1+x2=1-b,x1•x2=c,由x1>0,x2-x1>1,利用不等式的性质即可证明c=x1•x2>0;
(2)先求出b2-(2b+4c)=b2-2b-4c=(1-b)2-4c-1,再将x1+x2=1-b,x1•x2=c代入,得出b2-(2b+4c)=(x1+x2)2-4x1•x2-1=(x2-x1)2-1,由x2-x1>1,得出(x2-x1)2>1,进而得出b2>2b+4c;
(3)将c=
代入得y=x2+bx+
,由AB=2,A(x1,y1)、B(x2,y2),根据两点间的距离公式得出(x2-x1)2+(y2-y1)2=4,将y1=x1,y2=x2代入,得到(x2-x1)2=2,即(x1+x2)2-4x1•x2=2,再把x1+x2=1-b,x1•x2=c=
代入,得出(1-b)2-4×
=2,解方程求出b=-1或3,根据x1>0,x2-x1>1,得到x1+x2=1-b>1,b<0,于是确定b=-1,进而得到抛物线的解析式.
(2)先求出b2-(2b+4c)=b2-2b-4c=(1-b)2-4c-1,再将x1+x2=1-b,x1•x2=c代入,得出b2-(2b+4c)=(x1+x2)2-4x1•x2-1=(x2-x1)2-1,由x2-x1>1,得出(x2-x1)2>1,进而得出b2>2b+4c;
(3)将c=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:(1)证明:将y=x2+bx+c代入y=x,得x=x2+bx+c,
整理得x2+(b-1)x+c=0,
∵抛物线y=x2+bx+c与直线y=x交于A(x1,y1)、B(x2,y2)两点,
∴x1+x2=1-b,x1•x2=c,
∵x2-x1>1,
∴x2>x1+1,
∵x1>0,
∴x2>0,
∴c=x1•x2>0;
(2)解:∵b2-(2b+4c)=b2-2b-4c=(b-1)2-1-4c=(1-b)2-4c-1,
∵x1+x2=1-b,x1•x2=c,
∴b2-(2b+4c)=(x1+x2)2-4x1•x2-1=(x2-x1)2-1,
∵x2-x1>1,
∴(x2-x1)2>1,
∴b2-(2b+4c)>0,
∴b2>2b+4c;
(3)解:∵c=
,
∴y=x2+bx+
,
∵AB=2,A(x1,y1)、B(x2,y2),
∴(x2-x1)2+(y2-y1)2=4,
∵y1=x1,y2=x2,
∴(x2-x1)2=2,
∴(x1+x2)2-4x1•x2=2,
∵x1+x2=1-b,x1•x2=c=
,
∴(1-b)2-4×
=2,
∴b=-1或3,
∵x1>0,x2-x1>1,
∴x1+x2=1-b>1,
∴b<0,
∴b=-1,
∴抛物线的解析式是y=x2-x+
.
整理得x2+(b-1)x+c=0,
∵抛物线y=x2+bx+c与直线y=x交于A(x1,y1)、B(x2,y2)两点,
∴x1+x2=1-b,x1•x2=c,
∵x2-x1>1,
∴x2>x1+1,
∵x1>0,
∴x2>0,
∴c=x1•x2>0;
(2)解:∵b2-(2b+4c)=b2-2b-4c=(b-1)2-1-4c=(1-b)2-4c-1,
∵x1+x2=1-b,x1•x2=c,
∴b2-(2b+4c)=(x1+x2)2-4x1•x2-1=(x2-x1)2-1,
∵x2-x1>1,
∴(x2-x1)2>1,
∴b2-(2b+4c)>0,
∴b2>2b+4c;
(3)解:∵c=
| 1 |
| 2 |
∴y=x2+bx+
| 1 |
| 2 |
∵AB=2,A(x1,y1)、B(x2,y2),
∴(x2-x1)2+(y2-y1)2=4,
∵y1=x1,y2=x2,
∴(x2-x1)2=2,
∴(x1+x2)2-4x1•x2=2,
∵x1+x2=1-b,x1•x2=c=
| 1 |
| 2 |
∴(1-b)2-4×
| 1 |
| 2 |
∴b=-1或3,
∵x1>0,x2-x1>1,
∴x1+x2=1-b>1,
∴b<0,
∴b=-1,
∴抛物线的解析式是y=x2-x+
| 1 |
| 2 |
点评:本题考查了二次函数图象与系数的关系,二次函数与一元二次方程的关系,根与系数的关系,两点间的距离公式,不等式的性质,难度适中.

练习册系列答案
相关题目
 如图,数轴上线段AB=2cm,CD=4cm,点A在数轴上点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以6cm/s的速度向右匀速运动,同时线段CD以2cm/s的速度向左匀速运动.
如图,数轴上线段AB=2cm,CD=4cm,点A在数轴上点A在数轴上表示的数是-10,点C在数轴上表示的数是16.若线段AB以6cm/s的速度向右匀速运动,同时线段CD以2cm/s的速度向左匀速运动.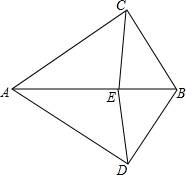 如图,BA平分∠CAD,BC⊥AC于C,BD⊥AD于D,E是AB上一点.
如图,BA平分∠CAD,BC⊥AC于C,BD⊥AD于D,E是AB上一点.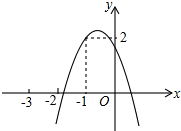 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论: