题目内容
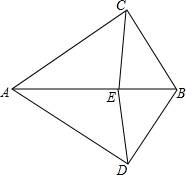 如图,BA平分∠CAD,BC⊥AC于C,BD⊥AD于D,E是AB上一点.
如图,BA平分∠CAD,BC⊥AC于C,BD⊥AD于D,E是AB上一点.(1)证明:EB平分∠CED;
(2)当E点在AB的延长线上或AB的反向延长线时,上述结论成立么?请证明.
考点:角平分线的性质,全等三角形的判定与性质
专题:
分析:(1)先由角平分线上的点到角两边的距离相等得出BC=BD,再利用HL证明Rt△ABC≌Rt△ABD,根据全等三角形的对应角相等得到∠ABC=∠ABD.再根据SAS证明△BCE≌△BDE,得出∠BEC=∠BED,即EB平分∠CED;
(2)当E点在AB的延长线上或AB的反向延长线时,上述结论仍然成立.当E点在AB的延长线上时,先由(1)知∠ABC=∠ABD,根据等角的补角相等得出∠EBC=∠EBD,再根据SAS证明△BCE≌△BDE,得出∠BEC=∠BED,即EB平分∠CED;当E点在AB的反向延长线时,先由(1)知∠ABC=∠ABD,BC=BD.再根据SAS证明△BCE≌△BDE,得出∠BEC=∠BED,即EB平分∠CED.
(2)当E点在AB的延长线上或AB的反向延长线时,上述结论仍然成立.当E点在AB的延长线上时,先由(1)知∠ABC=∠ABD,根据等角的补角相等得出∠EBC=∠EBD,再根据SAS证明△BCE≌△BDE,得出∠BEC=∠BED,即EB平分∠CED;当E点在AB的反向延长线时,先由(1)知∠ABC=∠ABD,BC=BD.再根据SAS证明△BCE≌△BDE,得出∠BEC=∠BED,即EB平分∠CED.
解答:(1)证明:∵BA平分∠CAD,BC⊥AC于C,BD⊥AD于D,
∴BC=BD.
在Rt△ABC和Rt△ABD中,
,
∴Rt△ABC≌Rt△ABD(HL),
∴∠ABC=∠ABD.
在△BCE和△BDE中,
,
∴△BCE≌△BDE(SAS),
∴∠BEC=∠BED,
即EB平分∠CED;
 (2)解:当E点在AB的延长线上或AB的反向延长线时,上述结论仍然成立.理由如下:
(2)解:当E点在AB的延长线上或AB的反向延长线时,上述结论仍然成立.理由如下:
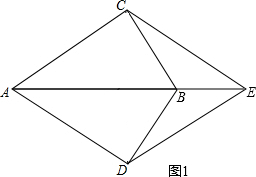
当E点在AB的延长线上时,如图1.
由(1)知∠ABC=∠ABD,BC=BD,
∴180°-∠ABC=180°-∠ABD,即∠EBC=∠EBD.
在△BCE和△BDE中,
,
∴△BCE≌△BDE(SAS),
∴∠BEC=∠BED,
即EB平分∠CED;
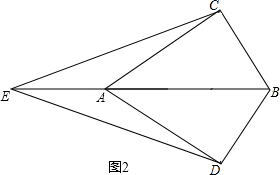 当E点在AB的反向延长线时,如图2.
当E点在AB的反向延长线时,如图2.
由(1)知∠ABC=∠ABD,BC=BD.
在△BCE和△BDE中,
,
∴△BCE≌△BDE(SAS),
∴∠BEC=∠BED,
即EB平分∠CED.
∴BC=BD.
在Rt△ABC和Rt△ABD中,
|
∴Rt△ABC≌Rt△ABD(HL),
∴∠ABC=∠ABD.
在△BCE和△BDE中,
|
∴△BCE≌△BDE(SAS),
∴∠BEC=∠BED,
即EB平分∠CED;
 (2)解:当E点在AB的延长线上或AB的反向延长线时,上述结论仍然成立.理由如下:
(2)解:当E点在AB的延长线上或AB的反向延长线时,上述结论仍然成立.理由如下:当E点在AB的延长线上时,如图1.
由(1)知∠ABC=∠ABD,BC=BD,
∴180°-∠ABC=180°-∠ABD,即∠EBC=∠EBD.
在△BCE和△BDE中,
|
∴△BCE≌△BDE(SAS),
∴∠BEC=∠BED,
即EB平分∠CED;
 当E点在AB的反向延长线时,如图2.
当E点在AB的反向延长线时,如图2.由(1)知∠ABC=∠ABD,BC=BD.
在△BCE和△BDE中,
|
∴△BCE≌△BDE(SAS),
∴∠BEC=∠BED,
即EB平分∠CED.
点评:本题考查了角平分线的性质,全等三角形的判定与性质,补角的性质,难度适中.正确画出图形利用数形结合是解题的关键.

练习册系列答案
相关题目
在函数y=
中,自变量x的取值范围是( )
| x-1 |
| A、x≤1 | B、x≥1 |
| C、x<1 | D、x>1 |
把多项式-3x2n-6xn分解因式,结果为( )
| A、-3xn(xn+2) |
| B、-3(x2n+2xn) |
| C、-3xn(x2+2) |
| D、3(-x2n-2xn) |