题目内容
圆锥的轴截面是一个边长为10cm的正三角形，则这个圆锥面的侧面积为 cm2，高为 cm．
考点：圆锥的计算
专题：计算题
分析：如图等边三角形SAB为圆锥的轴截面，根据等边三角形的性质得SA=AB=10cm，OA=5cm，则根据勾股定理可计算出圆锥的高SO=5
cm，然后根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式计算这个圆锥面的侧面积．
| 3 |
解答：解：如图，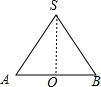
等边三角形SAB为圆锥的轴截面，SA=AB=10cm，
则OA=
AB=5cm，
所以SO=
=5
cm，
这个圆锥面的侧面积=
•2π•5•10=50π（cm2）．
故答案为50π，5
．
等边三角形SAB为圆锥的轴截面，SA=AB=10cm，则OA=
| 1 |
| 2 |
所以SO=
| AS2-AO2 |
| 3 |
这个圆锥面的侧面积=
| 1 |
| 2 |
故答案为50π，5
| 3 |
点评：本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
已知小球从点A运动到点B，速度v（米/秒）是时间t（秒）的正比例函数，3秒时小球的速度是6米/秒，那么速度v与时间t之间的关系式是（ ）
A、v=
| ||
B、v=
| ||
| C、v=3t | ||
| D、v=2t |
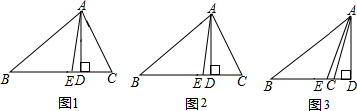
如图，在△ABC中，已知AB=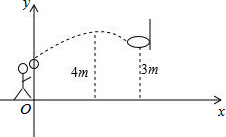
某校九年级的一场篮球比赛中，如图队员甲正在投篮，已知球出手时离地面高