题目内容
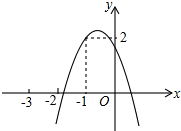 如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:
如图所示,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且与x轴交点的横坐标为别为x1,x2,其中-2<x1<-1,0<x2<1.下列结论:①2a-b<0;②a<
| b+c |
| 2 |
其中正确的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答: 解:①由图示知,∵抛物线开口方向向下,∴a<0,
解:①由图示知,∵抛物线开口方向向下,∴a<0,
又∵对称轴x=-
>-1.
∴b>2a,
∴2a-b<0.
故①正确;
②由①知,2a<b.
∵由图知,抛物线与y轴交于正半轴,则c>0,
∴2a<b+c,
∴a<
.
故②正确;
③由图知,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),则a-b+c=2,(1)
由已知得,0<x2<1.当x=1时,y<0,即a+b+c<0,(2)
由已知得,-2<x1<-1.当x=-2时,y<0,即4a-2b+c<0.(3)
联立(1)、(2)得到 a+c<1.(4)
联立(1)、(3)得到2a-c<-4,(5)
联立(4)、(5)得到3a<-3,
则a<-1.
故③正确;
④如图所示,∵二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且点(-1,2)不是顶点,
∴
>2,
∵a<0,
∴4ac-b2<8a.
∴b2+8a>4ac.
故④正确.
综上所述,正确的结论有4个.
故选:D.
 解:①由图示知,∵抛物线开口方向向下,∴a<0,
解:①由图示知,∵抛物线开口方向向下,∴a<0,又∵对称轴x=-
| b |
| 2a |
∴b>2a,
∴2a-b<0.
故①正确;
②由①知,2a<b.
∵由图知,抛物线与y轴交于正半轴,则c>0,
∴2a<b+c,
∴a<
| b+c |
| 2 |
故②正确;
③由图知,二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),则a-b+c=2,(1)
由已知得,0<x2<1.当x=1时,y<0,即a+b+c<0,(2)
由已知得,-2<x1<-1.当x=-2时,y<0,即4a-2b+c<0.(3)
联立(1)、(2)得到 a+c<1.(4)
联立(1)、(3)得到2a-c<-4,(5)
联立(4)、(5)得到3a<-3,
则a<-1.
故③正确;
④如图所示,∵二次函数y=ax2+bx+c(a≠0)的图象经过点(-1,2),且点(-1,2)不是顶点,
∴
| 4ac-b2 |
| 4a |
∵a<0,
∴4ac-b2<8a.
∴b2+8a>4ac.
故④正确.
综上所述,正确的结论有4个.
故选:D.
点评:主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式的熟练运用.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
把多项式-3x2n-6xn分解因式,结果为( )
| A、-3xn(xn+2) |
| B、-3(x2n+2xn) |
| C、-3xn(x2+2) |
| D、3(-x2n-2xn) |
 如图所示,有一圆柱形油罐,它的底面半径为10cm,高为17cm,一只蚂蚁从A点沿着油罐的表面爬行到点B处,已知点B到油罐顶部点C的距离为BC=2cm,求蚂蚁从点A处爬行到B处的最短路程是多少厘米?(π取3.14,结果精确到1cm,参考数据:
如图所示,有一圆柱形油罐,它的底面半径为10cm,高为17cm,一只蚂蚁从A点沿着油罐的表面爬行到点B处,已知点B到油罐顶部点C的距离为BC=2cm,求蚂蚁从点A处爬行到B处的最短路程是多少厘米?(π取3.14,结果精确到1cm,参考数据: