题目内容
13.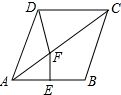 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )| A. | 66° | B. | 52° | C. | 104° | D. | 86° |
分析 连接BF,由菱形ABCD中,∠BAD的度数,则可求得∠FAB=∠FBA的度数,继而求得∠CBF的度数,然后由△DCF≌△BCF,求得答案.
解答 解:连接BF,
∵四边形ABCD是菱形,且∠BAD=76°,
∴∠EAF=$\frac{1}{2}$∠BAD=38°,CD=CB,∠DCF=∠BCF,
∵EF是AB的垂直平分线,
∴AF=BF,
∴∠EAF=∠EBF=38°,
∵AD∥BC,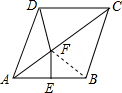
∴∠CBA=180°-∠BAD=104°,
∴∠CBF=∠CBA-∠ABF=104°-38°=66°,
在△CDF和△BCF中,
$\left\{\begin{array}{l}{CD=CB}\\{∠DCF=∠BCF}\\{CF=CF}\end{array}\right.$,
∴△DCF≌△BCF(SAS),
∴∠CDF=∠CBF=66°,
故选A.
点评 此题考查了菱形的性质、线段垂直平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.对于实数a、b,定义一种运算“?”为:a?b=a2+ab-2,有下列命题:
①1?3=2;②方程x?1=0的根为:x1=-2,x2=1;③不等式组$\left\{\begin{array}{l}{(-2)?x-4<0}\\{1?x-3<0}\end{array}\right.$的解集为:-1<x<4;④点(1,-2)在函数y=x?(-1)的图象上.
其中正确的是( )
①1?3=2;②方程x?1=0的根为:x1=-2,x2=1;③不等式组$\left\{\begin{array}{l}{(-2)?x-4<0}\\{1?x-3<0}\end{array}\right.$的解集为:-1<x<4;④点(1,-2)在函数y=x?(-1)的图象上.
其中正确的是( )
| A. | ①②③④ | B. | ①③④ | C. | ①②④ | D. | ①②③ |
5.下列变形正确的是( )
| A. | (a2)3=a9 | B. | 2a×3a=6a2 | C. | a6-a2=a4 | D. | 2a+3b=6ab |
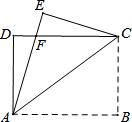 如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )
如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )