题目内容
8.现规定$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=a-b+c-d,试计算$|\begin{array}{l}{xy-3{x}^{2}}&{-2xy}\\{-2{x}^{2}}&{-5+xy}\end{array}|$,其中x=2,y=1.分析 原式利用题中的新定义化简,将x与y的值代入计算即可求出值.
解答 解:原式=(xy-3x2)-(-2xy)-2x2-(-5+xy)=xy-3x2+2xy-2x2+5-xy=-5x2+2xy+5,
当x=2,y=1时,原式=-20+4+5=-11.
点评 此题考查了整式的混合运算-化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
16.下列计算正确的是( )
| A. | 3a2-2a=a | B. | (-a2)3=a6 | C. | a÷a3=$\frac{1}{{a}^{2}}$ | D. | 2a2•3a2=5a4 |
13.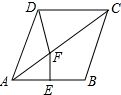 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )| A. | 66° | B. | 52° | C. | 104° | D. | 86° |
17. 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )
 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
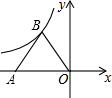 等边△OAB的边长为2,顶点A在x轴负半轴上,反比例函数y=$\frac{k}{x}$的图象经过顶点B,则k的值为y=-$\frac{\sqrt{3}}{x}$.
等边△OAB的边长为2,顶点A在x轴负半轴上,反比例函数y=$\frac{k}{x}$的图象经过顶点B,则k的值为y=-$\frac{\sqrt{3}}{x}$.