题目内容
3.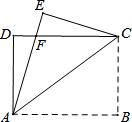 如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )
如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=$\frac{25}{4}$,则AD的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
分析 根据平行线的性质和翻转变换的性质得到FD=FE,FA=FC,根据勾股定理计算即可.
解答 解:∵DC∥AB,
∴∠FCA=∠CAB,又∠FAC=∠CAB,
∴∠FAC=∠FCA,
∴FA=FC=$\frac{25}{4}$,
∴FD=FE,
∵DC=AB=8,AF=$\frac{25}{4}$,
∴FD=FE=8-$\frac{25}{4}$=$\frac{7}{4}$,
∴AD=BC=EC=$\sqrt{F{C}^{2}-F{E}^{2}}$=6,
故选:D.
点评 本题考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
13.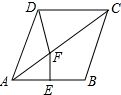 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )| A. | 66° | B. | 52° | C. | 104° | D. | 86° |
14.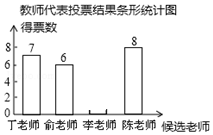 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?
 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).学生投票结果统计表
| 候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
| 得票数 | 460 | 200 | 140 | 300 |
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?
11.如果-22a2bcn是7次单项式,则n的值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 5 |
8.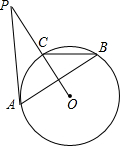 如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
 如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )
如图,PA与⊙O相切于点A,PO交⊙O于点C,点B是优弧CBA上一点,若∠P=26°,则∠ABC的度数为( )| A. | 26° | B. | 64° | C. | 32° | D. | 90° |
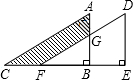 将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.
将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.