题目内容
4.小宇与小曼玩数字游戏,已知红色卡片有3张,上面分别标有数字4,5,6,黄色卡片有4张,上面分别标有数字3,5,6,7.(1)小宇和小曼分别从红色卡片和黄色卡片中随机抽取一张,若两数相乘的积为偶数,则小宇获胜;若相乘的积为奇数,则小曼获胜.小宇和小曼获胜的概率各是多少?这个游戏公平吗?
(2)若b,c分别是从红色卡片和黄色卡片所抽取的数字,求关于x的方程x2+bx+c=0有实数根的概率是多少?
分析 (1)依据题意先用列表法或画树状图法分析所有等可能的出现结果,然后计算出游戏双方赢的概率,概率相等则公平,否则不公平;
(2)若所给的一元二次方程有实数根,则方程的判别式△≥0,由此可得到满足条件b、c的组合总数,结合(1)即可求出其概率.
解答 解:(1)不公平,理由如下:
列表如下:
| 3 | 5 | 6 | 7 | |
| 4 | 12 | 20 | 24 | 28 |
| 5 | 15 | 25 | 30 | 35 |
| 6 | 18 | 30 | 36 | 42 |
所以这个游戏不公平;
(2)若x的方程x2+bx+c=0有实数根则△≥0,
即b2-4ac≥0,由(1)可知满足条件的b、c组合共有8种,
所以关于x的方程x2+bx+c=0有实数根的概率=$\frac{8}{12}$=$\frac{2}{3}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.游戏双方获胜的概率相同,游戏就公平,否则游戏不公平.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
14.已知a=2013,b=2014,则a2-2ab+b2的值为( )
| A. | 1 | B. | -1 | C. | ±1 | D. | 16216729 |
12.某中学为了解九年级学生的学习情况,抽取了200名学生的期末考试成绩进行统计分析,这200名学生的期末考试成绩中最高分是510分,最低分是450分,下列说法不正确的是( )
| A. | 抽取的200名学生的期末考试成绩的极差是60分 | |
| B. | 总体是抽取的200名学生的期末考试成绩 | |
| C. | 样本容量是200 | |
| D. | 个体是每个九年级学生的期末考试成绩 |
16.下列计算正确的是( )
| A. | 3a2-2a=a | B. | (-a2)3=a6 | C. | a÷a3=$\frac{1}{{a}^{2}}$ | D. | 2a2•3a2=5a4 |
13.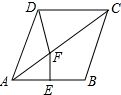 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )| A. | 66° | B. | 52° | C. | 104° | D. | 86° |
14.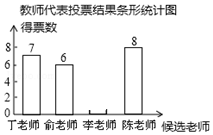 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?
 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).学生投票结果统计表
| 候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
| 得票数 | 460 | 200 | 140 | 300 |
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?