题目内容
2.从-$\frac{3}{2}$,-1,0,1这四个数中,任取一个数作为m的值,恰好使得关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-m}\\{x-y=2}\end{array}\right.$有整数解,且使以x为自变量的一次函数y=(m+1)x+3m-3的图象不经过第二象限,则取到满足条件的m值的概率为$\frac{1}{2}$.分析 首先由题意可求得满足条件的m值,然后直接利用概率公式求解即可求得答案.
解答 解:∵关于x,y的二元一次方程组$\left\{\begin{array}{l}{2x-y=-m}\\{x-y=2}\end{array}\right.$有整数解,
∴$\left\{\begin{array}{l}{x=-m-2}\\{y=-m-4}\end{array}\right.$,
∴m的值为:-1,0,1;
∵一次函数y=(m+1)x+3m-3的图象不经过第二象限,
∴$\left\{\begin{array}{l}{m+1>0}\\{3m-3≤0}\end{array}\right.$,
解得:-1<m≤1,
∴m的值为:0,1;
综上满足条件的m值为:0,1;
∴取到满足条件的m值的概率为:$\frac{2}{4}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了概率公式的应用、二元一次方程组的正整数解以及一次函数的性质.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
12.某中学为了解九年级学生的学习情况,抽取了200名学生的期末考试成绩进行统计分析,这200名学生的期末考试成绩中最高分是510分,最低分是450分,下列说法不正确的是( )
| A. | 抽取的200名学生的期末考试成绩的极差是60分 | |
| B. | 总体是抽取的200名学生的期末考试成绩 | |
| C. | 样本容量是200 | |
| D. | 个体是每个九年级学生的期末考试成绩 |
13.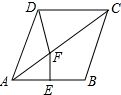 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
 如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )
如图,菱形ABCD中,∠BAD=76°,AB的垂直平分线EF交AC于F,则∠CDF的度数为( )| A. | 66° | B. | 52° | C. | 104° | D. | 86° |
10. 如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( )
如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( )
 如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( )
如图,矩形ABCD的外接圆O与水平地面相切于点A,已知圆O的半径为4,且$\widehat{BC}$=2$\widehat{AB}$.若在没有滑动的情况下,将圆O向右滚动,使得O点向右移动了66π,则此时与地面相切的弧为( )| A. | $\widehat{AB}$ | B. | $\widehat{BC}$ | C. | $\widehat{CD}$ | D. | $\widehat{DA}$ |
17. 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )
 如图所示,该几何体的主视图是( )
如图所示,该几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
7.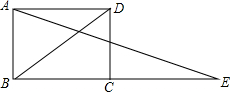 如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )
如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )
 如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )
如图,在矩形ABCD中,AB=2,AD=2$\sqrt{3}$,点E在BC的延长线上,且BD=CE,连接AE,则∠E的度数为( )| A. | 15° | B. | 20° | C. | 30° | D. | 45° |
14.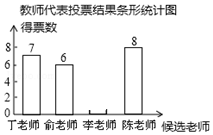 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
学生投票结果统计表
(1)若共有25位教师代表参加投票,则李老师得到的教师票数是多少?请补全条形统计图.(画在答案卷相对应的图上)
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?
 某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).
某校开展了“我最喜爱的老师”评选活动.确定如下评选方案:有学生和教师代表对4名候选教师进行投票,每票选1名候选教师,每位候选教师得到的教师票数的5倍与学生票数的和作为该教师的总票数.以下是根据学生和教师代表投票结果绘制的统计表和条形统计图(不完整).学生投票结果统计表
| 候选教师 | 丁老师 | 俞老师 | 李老师 | 陈老师 |
| 得票数 | 460 | 200 | 140 | 300 |
(2)丁老师与李老师得到的学生总票数是600,且丁老师得到的学生票数是李老师得到的学生票数的3倍多40票,求丁老师与李老师得到的学生票数分别是多少?
(3)在(1)、(2)的条件下,若总得票数较高的2名教师推选到市参评,你认为推选到市里的是两位老师?为什么?
11.如果-22a2bcn是7次单项式,则n的值是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 5 |
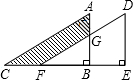 将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.
将直角三角形ABC沿CB方向平移BE的距离后,得到直角三角形DEF,已知AG=4,BE=6,DE=12,求阴影部分的面积.