题目内容
1．计算：$\sqrt{12}$-3$\sqrt{\frac{1}{3}}$+tan30°=$\frac{4\sqrt{3}}{3}$．分析 原式前两项化为最简二次根式，最后一项利用特殊角的三角函数值计算即可得到结果．
解答 解：原式=2$\sqrt{3}$-$\sqrt{3}$+$\frac{\sqrt{3}}{3}$=$\frac{4\sqrt{3}}{3}$，
故答案为：$\frac{4\sqrt{3}}{3}$
点评 此题考查了实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
11．如果从1、2、3、4、5、6、7、8、9、10这十个数中随机取出一个数，那么取出的数是3的倍数的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{5}$ | D． | $\frac{3}{10}$ |
12．某中学为了解九年级学生的学习情况，抽取了200名学生的期末考试成绩进行统计分析，这200名学生的期末考试成绩中最高分是510分，最低分是450分，下列说法不正确的是（ ）
| A． | 抽取的200名学生的期末考试成绩的极差是60分 | |
| B． | 总体是抽取的200名学生的期末考试成绩 | |
| C． | 样本容量是200 | |
| D． | 个体是每个九年级学生的期末考试成绩 |
16．下列计算正确的是（ ）
| A． | 3a2-2a=a | B． | （-a2）3=a6 | C． | a÷a3=$\frac{1}{{a}^{2}}$ | D． | 2a2•3a2=5a4 |
13．
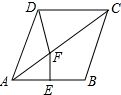如图，菱形ABCD中，∠BAD=76°，AB的垂直平分线EF交AC于F，则∠CDF的度数为（ ）
如图，菱形ABCD中，∠BAD=76°，AB的垂直平分线EF交AC于F，则∠CDF的度数为（ ）| A． | 66° | B． | 52° | C． | 104° | D． | 86° |
10．
如图，矩形ABCD的外接圆O与水平地面相切于点A，已知圆O的半径为4，且$\widehat{BC}$=2$\widehat{AB}$．若在没有滑动的情况下，将圆O向右滚动，使得O点向右移动了66π，则此时与地面相切的弧为（ ）
如图，矩形ABCD的外接圆O与水平地面相切于点A，已知圆O的半径为4，且$\widehat{BC}$=2$\widehat{AB}$．若在没有滑动的情况下，将圆O向右滚动，使得O点向右移动了66π，则此时与地面相切的弧为（ ）| A． | $\widehat{AB}$ | B． | $\widehat{BC}$ | C． | $\widehat{CD}$ | D． | $\widehat{DA}$ |
11．如果-22a2bcn是7次单项式，则n的值是（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 5 |