题目内容
 如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止;点Q以2cm/s的速度向点D移动,设运动的时间为t.
如图,A、B、C、D为矩形的四个顶点,AB=16cm,BC=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达点B为止;点Q以2cm/s的速度向点D移动,设运动的时间为t.(1)t为何值时,四边形APQD为矩形?
(2)t为何值时,P、Q两点之间的距离是6
| 5 |
(3)在移动的过程中,PQ能否将矩形ABCD分成面积比为1:2的两部分?若能,求出t的值;若不能,说明理由.
考点:一元二次方程的应用
专题:几何动点问题
分析:(1)根据矩形的性质,根据等量关系:AP=DQ,列出方程即可求解;
(2)根据勾股定理,根据等量关系:P、Q两点之间的距离是6
m,列出方程即可求解;
(3)分两种情况:梯形ADQP的面积:矩形ABCD的面积=1:3;梯形BCQP的面积:矩形ABCD的面积=2:3;进行讨论即可求解.
(2)根据勾股定理,根据等量关系:P、Q两点之间的距离是6
| 5 |
(3)分两种情况:梯形ADQP的面积:矩形ABCD的面积=1:3;梯形BCQP的面积:矩形ABCD的面积=2:3;进行讨论即可求解.
解答:解:(1)依题意有
3t=16-2t,
解得t=3.2.
故t为3.2s时,四边形APQD为矩形.
(2)依题意有
(3t-16+2t)2+62=(6
)2,
解得t1=5.6(不合题意舍去),t2=0.8.
故t为0.8时,P、Q两点之间的距离是6
m.
(3)梯形ADQP的面积:矩形ABCD的面积=1:3,依题意有
3t(16-2t):(16×6)=1:3,
解得t1=
(不合题意舍去),t2=
;
梯形BCQP的面积:矩形ABCD的面积=2:3,依题意有
3t(16-2t):(16×6)=2:3,
解得t1=
(不合题意舍去),t2=
.
故t的值是
或
.
3t=16-2t,
解得t=3.2.
故t为3.2s时,四边形APQD为矩形.
(2)依题意有
(3t-16+2t)2+62=(6
| 5 |
解得t1=5.6(不合题意舍去),t2=0.8.
故t为0.8时,P、Q两点之间的距离是6
| 5 |
(3)梯形ADQP的面积:矩形ABCD的面积=1:3,依题意有
3t(16-2t):(16×6)=1:3,
解得t1=
12+4
| ||
| 3 |
12-4
| ||
| 3 |
梯形BCQP的面积:矩形ABCD的面积=2:3,依题意有
3t(16-2t):(16×6)=2:3,
解得t1=
12+4
| ||
| 3 |
12-4
| ||
| 3 |
故t的值是
12-4
| ||
| 3 |
12-4
| ||
| 3 |
点评:本题考查了一元二次方程的应用,矩形的性质及判定,勾股定理,梯形的面积等知识,综合性较强,利用数形结合、分类讨论及方程思想是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
若(a2+b2-2)(a2+b2)+1=0,则a2+b2的值为( )
| A、-2 | B、5 | C、2 | D、1 |
已知xm=6,xn=3,则x2m-3n的值为( )
A、
| ||
B、
| ||
| C、12 | ||
| D、9 |
 “五一节”期间,一个家庭自驾游去了离家170千米的某地,如图分别是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,他们出发2小时时,离目的地还有
“五一节”期间,一个家庭自驾游去了离家170千米的某地,如图分别是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象,他们出发2小时时,离目的地还有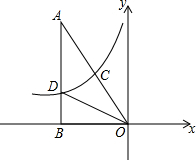 如图,Rt△OAB与曲线y1=
如图,Rt△OAB与曲线y1= 墨墨的爸爸将一块长为(
墨墨的爸爸将一块长为(
 如图所示,△ABC与△DEF是两个全等的等腰直角三角形,BC=EF=8,∠C=∠F=90°,且点C、E、B、F在同一条直线上,将△ABC沿CB方向平移,设AB与DE相交于P点,设CE=x,△PBE的面积为S,求:
如图所示,△ABC与△DEF是两个全等的等腰直角三角形,BC=EF=8,∠C=∠F=90°,且点C、E、B、F在同一条直线上,将△ABC沿CB方向平移,设AB与DE相交于P点,设CE=x,△PBE的面积为S,求: