Question

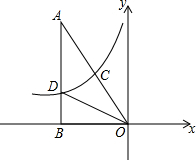如图，Rt△OAB与曲线y₁=

k

x

的一支交于点C、D，点B在横轴上，AC=OC，△BOD∽△BAO；
（1）求直线OA的解析式y₂；
（2）若△AOD的面积为9，求k的值；
（3）直接写出y₁＞y₂时x的取值范围．

Answer 1

考点：反比例函数综合题

专题：综合题

分析：（1）过点C作CE⊥x轴于E，根据反比例函数比例系数的几何意义可得S_△CEO=S_△DBO，易证△CEO∽△ABO，
根据相似三角形的性质可得

S△CEO

S△ABO

=

1

4

，从而得到

S△DBO

S△ABO

=

DB

AB

=

1

4

．再由△BOD∽△BAO可得BO²=BD•BA．设DB=a，可求得点A（-2a，4a），设直线OA的解析式y₂=kx，把点A的坐标代入y₂=kx，即可求出直线OA的解析式；
（2）由（1）中DB=a，AB=4a可得AD=3a，则有

S△ADO

S△BDO

=

AD

BD

=3，由S_△AOD=9可求得S_△BDO=3，由此可求出k的值；
（3）可先求出两个函数图象的交点坐标，然后数形结合就可解决问题．

解答：解：（1）过点C作CE⊥x轴于E，如图，
则有∠CEO=∠ABO=90°，
∴S_△CEO=S_△DBO=

1

2

.

k

.

，CE∥AB，
∴△CEO∽△ABO，
∴

S△CEO

S△ABO

=（

OC

OA

）²=

1

4

，
∴

S△DBO

S△ABO

=

DB

AB

=

1

4

．
∵△BOD∽△BAO，
∴

BO

BA

=

BD

BO

，即BO²=BD•BA．
设DB=a，则有AB=4a，从而有BO=2a，
∴点A（-2a，4a）．
设直线OA的解析式y₂=kx，
∴4a=-2ak，
∴k=-2，
∴直线OA的解析式y₂=-2x；

（2）由（1）中DB=a，AB=4a得AD=3a，
∴

S△ADO

S△BDO

=

AD

BD

=3．
∵S_△AOD=9，
∴S_△BDO=3，
∴

1

2

.

k

.

=3，
∴k=-6（舍正）；

（2）当y₁＞y₂时，x的取值范围为-

3

＜x＜0或x＞

3

．
提示：可先求出直线y=-2x与双曲线y=-

6

x

的交点坐标，为（-

3

，2

3

）、（

3

，-2

3

）；
然后画出两个函数完整图象，结合图象就可得到x的取值范围．

点评：本题主要考查了反比例函数比例系数的几何意义、求直线及双曲线的解析式、面积法、相似三角形的判定与性质等知识，还考查了数形结合的思想．关于两个三角形面积之比的问题，若两个三角形相似，可用相似三角形的面积比等于相似比的平方；若两个三角形两边所对的高相等，可用三角形的面积比等于这两边的比．