Question

5．在⊙O中，BC为直径，A为$\widehat{BC}$的中点，点D在AC上运动（与点A、C不重合），AC与BD交于点E，连接AD．

（1）如图1，求证：∠ADB=45°；
（2）如图2，点F在BD弦上，∠AFB=135°，连接CD，求证：BF=CD；
（3）在（2）的条件下，连接AO，当AE=CE时，求tan∠FAO的值．

Answer 1

分析 （1）首先根据直径的性质，证明∠C=45°，根据∠ADB=∠C即可解决问题．
（2）如图2中，连接AB、AO．欲证明BF=CD，只要证明△ABF≌△ACD即可．
（3）如图2中，首先证明∠FAO=∠ABE，根据tan∠FAO=tan∠ABE=$\frac{AE}{AB}$，结合条件即可解决问题．

解答 （1）证明：如图1中，连接AB，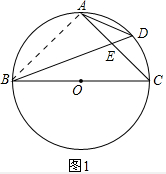

∵BC是直径，
∴∠BAC=90，
∵$\widehat{AB}$=$\widehat{AC}$，
∴AB=AC，
∴∠ABC=∠C=45°，
∴∠ADB=∠C=45°．

（2）如图2中，连接AB、AO．

∵∠AFB=135°，
∴∠AFD=180°-∠AFB=45°，
∵∠ADB=45°，
∴∠AFD=∠ADF=45°，
∴AF=AD，
∴∠FAD=∠BAC=90°，
∴∠BAF=∠CAD，
在△ABF和△ACD中，
$\left\{\begin{array}{l}{AB=AC}\\{∠BAF=∠CAD}\\{AF=AD}\end{array}\right.$，
∴△ABF≌△ACD，
∴BF=CD．

（3）在图中，∵∠BAF=∠CAD=∠CBD，
∵∠FAO+∠BAF=∠CBD+∠ABF=45°，
∴∠ABE=∠FAO，
∵AB=AC，AE=EC，
∴AB=2AE，
∴tan∠FAO=tan∠ABE=$\frac{AE}{AB}$=$\frac{1}{2}$．

点评 本题考查圆综合题、全等三角形判定和性质、锐角三角函数等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．