题目内容
9.已知一个平行四边形周长为20,两组对边之间的距离分别为2和3,则这个平行四边形的面积为12.分析 设出平行四边形的相邻两边的长度,根据周长已知列出方程.再利用各边计算面积列出另一方程,解出各边的长度,再计算平行四边形的面积.
解答 解:设平行四边形的边长为x,y.
则2(x+y)=20;
2x=3y,
联立解得y=4.
故平行四边形的面积为3y=12.
故答案为12.
点评 此题主要考查了平行四边形的性质,平行四边形的面积等于平行四边形的边长与该边上的高的积.即S=a•h.其中a可以是平行四边形的任何一边,h必须是a边与其对边的距离,即对应的高.

练习册系列答案
相关题目
14.若3ax2+$\frac{b}{3}$x+4=3x2-x+4对于任何x都成立,则a+b等于( )
| A. | 2 | B. | -2 | C. | 1 | D. | -1 |
1.二次函数y=(m-2)x2+m2+2m-8中,当x=0时,y=0,那么当x=2时,y的值应为( )
| A. | 2 | B. | -24 | C. | 24 | D. | -2 |
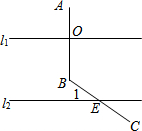 如图,l1∥l2,AB⊥l1,垂足为O,BC交l2于点E,若∠ABC=140°,求∠1的度数.
如图,l1∥l2,AB⊥l1,垂足为O,BC交l2于点E,若∠ABC=140°,求∠1的度数.