题目内容
19. 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
分析 由相似三角形的判定方法得出选项A、B、C能判断△CAB∽△CED,选项D不能判断△CAB∽△CED;即可得出结果.
解答 解:A、∵∠CDE=∠B,∠C=∠C,
∴△CAB∽△CED,
∴选项A能判断△CAB∽△CED;
B、∵∠CED=∠A,∠C=∠C,
∴△CAB∽△CED,
∴选项B能判断△CAB∽△CED;
C、∵$\frac{CD}{CE}=\frac{CB}{CA}$,∠C=∠C,
∴△CAB∽△CED,
∴选项C能判断△CAB∽△CED;
D、由$\frac{CD}{CA}=\frac{CE}{AB}$,∠C=∠C,
不能判断△CAB∽△CED;
故选:D.
点评 本题考查了相似三角形的判定方法;熟记相似三角形的判定方法是解决问题的关键.

练习册系列答案
相关题目
7. 如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
 如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
8.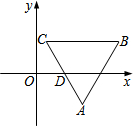 如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
 如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )| A. | (2$\sqrt{3}$,-$\sqrt{3}$) | B. | ($\sqrt{3}$-1,$\sqrt{3}$) | C. | ($\sqrt{3}$+1,-$\sqrt{3}$) | D. | ($\sqrt{3}$-1,-$\sqrt{3}$) |
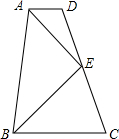 如图,在梯形ABCD中,AD∥BC,E为CD的中点,AD+BC=AB.则:
如图,在梯形ABCD中,AD∥BC,E为CD的中点,AD+BC=AB.则: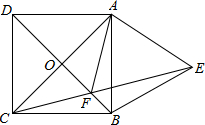 如图,已知正方形ABCD,以AB为边向外作等边三角形ABE,CE与DB相交于点F,则∠AFD的度数60°.
如图,已知正方形ABCD,以AB为边向外作等边三角形ABE,CE与DB相交于点F,则∠AFD的度数60°. 如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )
如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )
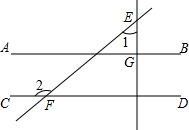 如图,已知直线AB∥CD,直线EG垂直于AB,垂足为G,直线EF交CD于点F,∠1=50°,则∠2=140°.
如图,已知直线AB∥CD,直线EG垂直于AB,垂足为G,直线EF交CD于点F,∠1=50°,则∠2=140°.