题目内容
10.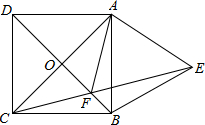 如图,已知正方形ABCD,以AB为边向外作等边三角形ABE,CE与DB相交于点F,则∠AFD的度数60°.
如图,已知正方形ABCD,以AB为边向外作等边三角形ABE,CE与DB相交于点F,则∠AFD的度数60°.
分析 根据正方形及等边三角形的性质求得∠AFE,∠BFE的度数,再根据三角形外角的性质即可求得答案.
解答 解:∵∠CBA=90°,∠ABE=60°,
∴∠CBE=150°,
∵四边形ABCD为正方形,三角形ABE为等边三角形
∴BC=BE,
∴∠BEC=15°,
∵∠FBE=∠DBA+∠ABE=105°,
∴∠BFE=60°,
在△CBF和△ABF中,
$\left\{\begin{array}{l}{BF=BF}\\{∠CBF=∠ABF}\\{BC=BA}\end{array}\right.$,
∴△CBF≌△ABF(SAS),
∴∠BAF=∠BCE=15°,
又∵∠ABF=45°,且∠AFD为△AFB的外角,
∴∠AFD=∠ABF+∠FAB=15°+45°=60°.
故答案为60°.
点评 本题考查等边三角形的性质、等腰三角形的性质及三角形内角和定理的综合运用,关键是根据正方形及等边三角形的性质求得∠AFE,∠BFE的度数.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
20.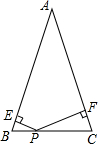 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )| A. | 2.5cm | B. | 2$\sqrt{2}$cm | C. | 5cm | D. | 2$\sqrt{3}$cm |
1.下列各组中的两项,不是同类项的是( )
| A. | 23与32 | B. | m2n与$-\frac{1}{2}m{n^2}$ | C. | 2πR与π2R | D. | -x2y与2yx2 |
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
15.与$\sqrt{3}$+1最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.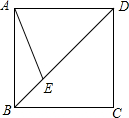 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | 4-2$\sqrt{2}$ |
19. 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).