题目内容
4. 如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )
如图,将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE,点M、N分别是BD、GE的中点,若BC=14,CE=2,则MN的长( )| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
分析 连接AC、CF、AF,由矩形的性质和勾股定理求出AC,由矩形的性质得出M是AC的中点,N是CF的中点,证出MN是△ACF的中位线,由三角形中位线定理得出MN=$\frac{1}{2}$AF,由等腰直角三角形的性质得出AF=$\sqrt{2}$AC=20,即可得出结果.
解答 解:连接AC、CF、AF,如图所示:
∵矩形ABCD绕点C顺时针旋转90°得到矩形FFCE,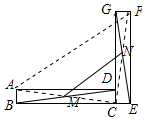
∴∠ABC=90°,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+1{4}^{2}}$=10$\sqrt{2}$,
AC=BD=GE=CF,AC与BD互相平分,GE与CF互相平分,
∵点M、N分别是BD、GE的中点,
∴M是AC的中点,N是CF的中点,
∴MN是△ACF的中位线,
∴MN=$\frac{1}{2}$AF,
∵∠ACF=90°,
∴△ACF是等腰直角三角形,
∴AF=$\sqrt{2}$AC=10$\sqrt{2}$×$\sqrt{2}$=20,
∴MN=10.
故选:D.
点评 本题考查了矩形的性质、旋转的性质、勾股定理、等腰直角三角形的判定与性质、三角形中位线定理;熟练掌握矩形的性质,由三角形中位线定理求出MN是解决问题的关键.

练习册系列答案
相关题目
15.与$\sqrt{3}$+1最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
19. 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
13.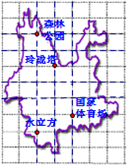 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
14.在下列二次根式中,与$\sqrt{a}$是同类二次根式的是( )
| A. | $\sqrt{2a}$ | B. | $\sqrt{3{a}^{2}}$ | C. | 2$\sqrt{a}$ | D. | $\sqrt{{a}^{4}}$ |
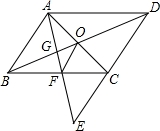 如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.
如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.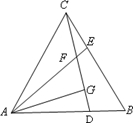 如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.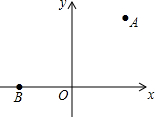 如图,在平面直角坐标系中,已知点A(3,4),B(-3,0).
如图,在平面直角坐标系中,已知点A(3,4),B(-3,0). 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)