题目内容
8.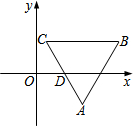 如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )
如图,在平面直角坐标系中,△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),则点A的坐标为( )| A. | (2$\sqrt{3}$,-$\sqrt{3}$) | B. | ($\sqrt{3}$-1,$\sqrt{3}$) | C. | ($\sqrt{3}$+1,-$\sqrt{3}$) | D. | ($\sqrt{3}$-1,-$\sqrt{3}$) |
分析 根据等边三角形的轴对称性质得到点D,由此求得点A的坐标.
解答 解:因为△ABC是等边三角形,BC∥x轴,AB=4,AC的中点D在x轴上,且D($\sqrt{3}$,0),
所以可得点A的纵坐标为-$\frac{1}{2}×2\sqrt{3}=-\sqrt{3}$,横坐标为$\sqrt{3}+1$.
故选C.
点评 本题考查了等边三角形的性质和坐标与图形性质,熟练掌握等边三角形的轴对称性质是解题的关键.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
19. 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
3.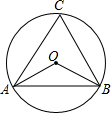 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
13.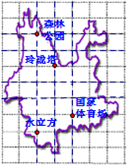 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
 我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )
我市为了促进全民健身,举办“健步走”活动,朝阳区活动场地位于奥林匹克公园(路线:森林公园-玲珑塔-国家体育场-水立方).如图,体育局的工作人员在奥林匹克公园设计图上设定玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),则终点水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
17.下列图形中,轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上) 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5). 如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.
如图,a∥b,直线c与直线a,b相交,已知∠1=110°,则∠2=70°.