题目内容
11.实践与操作:我们在学习四边形的相关知识时,认识了平行四边形、矩形、菱形、正方形等一些特殊的四边形,下面我们用尺规作图的方法来体会它们之间的联系.如图,在?ABCD中,AB=4,BC=6,∠ABC=60°,请完成下列任务:(1)在图1中作一个菱形,使得点A、B为所作菱形的2个顶点,另外2个顶点在?ABCD的边上;在图2中作一个菱形,使点B、D为所作菱形的2个顶点,另外2个顶点在?ABCD的边上;(尺规作图,保留作图痕迹,不写作法)
(2)请在图形下方横线处直接写出你按(1)中要求作出的菱形的面积.
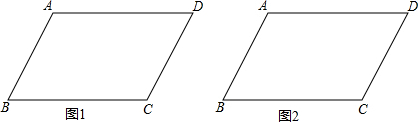
分析 (1)如图1,在AD、BC上分别截取AF=BE=4,连结EF,则四边形ABEF是菱形;
如图2,连结BD,作BD的垂直平分线,交AD于E,BC于F,则四边形BEDF是菱形;
(2)如图1,作?ABCD的高AH,根据菱形的面积=底×高列式计算即可;
如图2,设BD与EF交于点O,作DM⊥BC于M,则CM=BH=2,DM=AH=2$\sqrt{3}$.分别求出BD与EF,根据菱形的面积=两对角线乘积的一半列式计算即可.
解答 解:(1)如图所示:
(2) 如图1,作?ABCD的高AH.
如图1,作?ABCD的高AH.
在直角△ABH中,∵AB=4,∠ABC=60°,
∴AH=AB•sin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,BH=AB•cos60°=4×$\frac{1}{2}$=2,
∴S菱形ABEF=BE•AH=4×2$\sqrt{3}$=8$\sqrt{3}$;
如图2,设BD与EF交于点O,作DM⊥BC于M,则CM=BH=2,DM=AH=2$\sqrt{3}$.
在直角△BDM中,∵∠M=90°,
∴BD=$\sqrt{B{M}^{2}+D{M}^{2}}$=$\sqrt{(6+2)^{2}+(2\sqrt{3})^{2}}$=2$\sqrt{19}$.
设BF=x,CF=y,则DF=x,
由题意得$\left\{\begin{array}{l}{x+y=6}\\{{x}^{2}=(y+2)^{2}+(2\sqrt{3})^{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{19}{4}}\\{y=\frac{5}{4}}\end{array}\right.$,
∴OF=$\sqrt{B{F}^{2}-O{B}^{2}}$=$\sqrt{(\frac{19}{4})^{2}-(\sqrt{19})^{2}}$=$\frac{\sqrt{57}}{4}$,
∴S菱形ABEF=$\frac{1}{2}$BD•EF=$\frac{1}{2}$×2$\sqrt{19}$×$\frac{\sqrt{57}}{2}$=$\frac{19\sqrt{3}}{2}$.
点评 本题考查了菱形的判定与性质,平行四边形的性质,作图-复杂作图,熟练掌握定理是解题的关键.

 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 23与32 | B. | m2n与$-\frac{1}{2}m{n^2}$ | C. | 2πR与π2R | D. | -x2y与2yx2 |
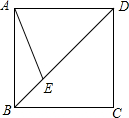 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | 4-2$\sqrt{2}$ |
 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
 如图,OA在x轴上,OB在y轴上,OA=4,OB=3,点C在边OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k的值是( )
如图,OA在x轴上,OB在y轴上,OA=4,OB=3,点C在边OA上,AC=1,⊙P的圆心P在线段BC上,且⊙P与边AB,AO都相切.若反比例函数y=$\frac{k}{x}$(k≠0)的图象经过圆心P,则k的值是( )| A. | $-\frac{5}{4}$ | B. | $-\frac{5}{3}$ | C. | $-\frac{5}{2}$ | D. | -2 |
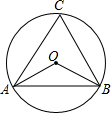 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上) 如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).
如图,在平面直角坐标系xOy中,直线y=x+b与双曲线y=$\frac{k}{x}$相交于A,B两点,已知A(2,5).