题目内容
7. 如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )
如图:已知△ABC为直角三角形,分别以直角边AC、BC为直径作半圆AmC和BnC,以AB为直径作半圆ACB,记两个月牙形阴影部分的面积之和为S1,△ABC的面积为S2,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 不能确定 |
分析 根据题给图形可知:S1=$\frac{1}{2}$π($\frac{1}{2}$AC)2+$\frac{1}{2}$π($\frac{1}{2}$BC)2-$\frac{1}{2}$π($\frac{1}{2}$AB)2+S△ABC,S2=S△ABC,在Rt△ABC中BC2+AC2=AB2,继而即可得出答案.
解答 解:在Rt△ABC中,
∵BC2+AC2=AB2,
∴S1=$\frac{1}{2}$π($\frac{1}{2}$AC)2+$\frac{1}{2}$π($\frac{1}{2}$BC)2-$\frac{1}{2}$π($\frac{1}{2}$AB)2+S△ABC=$\frac{1}{8}$π(BC2+AC2-AB2)+S△ABC=S△ABC,
S2=S△ABC.
∴S1=S2.
故选C.
点评 本题考查的是勾股定理,根据题意得出阴影部分的面积与直角三角形三条边的关系是解答此题的关键.

练习册系列答案
相关题目
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
15.与$\sqrt{3}$+1最接近的整数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
2.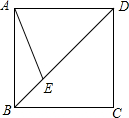 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | 4-2$\sqrt{2}$ |
19. 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
17.下列图形中,轴对称图形有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
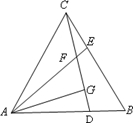 如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D、E分别为AB、BC边上的两个动点,且总有AD=BE,AE与CD交于点F,AG⊥CD于点G. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)
如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E,F分别在边BC和CD上,下列结论:①CE=CF=$\sqrt{2}$;②∠BAE=15°;③BE+DF=EF;④S正方形ABCD=2+$\sqrt{3}$.其中正确的序号是①②④(把你认为正确的都填上)