题目内容
9.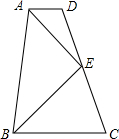 如图,在梯形ABCD中,AD∥BC,E为CD的中点,AD+BC=AB.则:
如图,在梯形ABCD中,AD∥BC,E为CD的中点,AD+BC=AB.则:(1)AE、BE分别平分∠DAB、∠ABC吗?为什么?
(2)AE⊥BE吗?为什么?
分析 (1)AE、BE分别平分∠DAB、∠ABC.延长AE、BC交于点F,先证明△ADE≌△FCE,再证明△ABF是等腰三角形,利用三线合一即可解决问题.
(2)利用三线合一即可解决.
解答 (1)解:AE、BE分别平分∠DAB、∠ABC.
理由:延长AE、BC交于点F.
∵AD∥BF,
∴∠D=∠ECF,
在△ADE和△FCE中,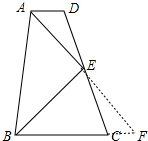
$\left\{\begin{array}{l}{∠D=∠ECF}\\{DE=EC}\\{∠AED=∠CEF}\end{array}\right.$,
∴△ADE≌△FCE,
∴AD=CF,∠DAE=∠F,AE=EF,
∵AD+BC=AB,
∴BC+CF=BC+AD=BF=AB,
∵AB=BF,AE=EF,
∴BE平分∠ABF,∠BAF=∠BFA=∠DAE,
∴EA平分∠DAB.
(2)结论:BE⊥AE.
证明:由(1)可知:BA=BF,AE=EF,
∴BE⊥AF(三线合一),
即BE⊥AE.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、角平分线的定义等知识,解题的关键是添加辅助线构造全等三角形,记住这种辅助线的添加方法,属于中考常考题型.

练习册系列答案
相关题目
20.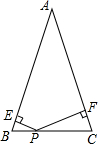 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
 如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )
如图,已知等腰三角形ABC中,AB=AC=10cm,∠A=30°,P是BC上一点,PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE+PF=( )| A. | 2.5cm | B. | 2$\sqrt{2}$cm | C. | 5cm | D. | 2$\sqrt{3}$cm |
1.下列各组中的两项,不是同类项的是( )
| A. | 23与32 | B. | m2n与$-\frac{1}{2}m{n^2}$ | C. | 2πR与π2R | D. | -x2y与2yx2 |
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
19. 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
 如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )
如图,在△ABC中,点D、E分别在边AC、BC上,下列条件中不能判断△CAB∽△CED的是( )| A. | ∠CDE=∠B | B. | ∠CED=∠A | C. | $\frac{CD}{CE}=\frac{CB}{CA}$ | D. | $\frac{CD}{CA}=\frac{CE}{AB}$ |
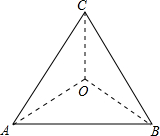 如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.
如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.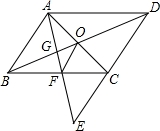 如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.
如图,E是?ABCD的边DC延长线上的一点,且CE=DC,连接AE,分别交BC、BD于点F、G,连接AC交BD于点O,连接OF,求证:AB=2OF.