题目内容
16. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,则线段EF的长度( )
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F,则线段EF的长度( )| A. | 线段EF的长度不变 | B. | 随D点的运动而变化,最小值为4$\sqrt{3}$ | ||
| C. | 随D点的运动而变化,最小值为2$\sqrt{3}$ | D. | 随D点的运动而变化,没有最值 |
分析 根据“点到直线之间,垂线段最短”可得CD⊥AB时CD最小,由于EF=2CD,求出CD的最小值就可求出EF的最小值.
解答 解:当CD⊥AB时,
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=8,∠CBA=30°,
∴∠CAB=60°,AC=4,BC=4$\sqrt{3}$.
∵CD⊥AB,∠CBA=30°,
∴CD=$\frac{1}{2}$BC=2$\sqrt{3}$.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为2$\sqrt{3}$.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为4$\sqrt{3}$,
故选B
点评 本题考查了轴对称的性质,关键是求出CD的最小值.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
7. 如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )
 如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )
如图,点P是△ABC外的一点,PD⊥AB于点D,PE⊥AC于点E,PF⊥BC于点F,连接PB,PC.若PD=PE=PF,∠BAC=70°,则∠BPC的度数为( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
4.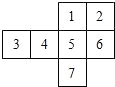 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
 将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )
将如图所示的图形剪去一个小正方形,使余下的部分恰好能折成一个正方体,应剪去(序号)( )| A. | 1或2或3 | B. | 3或4或5 | C. | 4或5或6 | D. | 1或2或6 |
8. 如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )
如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )
 如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )
如图,网格中小正方形的边长为1,点A、B为网格线的交点,则AB的长为( )| A. | 3 | B. | 5 | C. | 7 | D. | 12 |
 如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数.
如图,∠AOB=124°,OC是∠AOB的平分线,∠1与∠2互余,求∠1和∠BOD的度数. 如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
如图,小正方形的边长均为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )



 如图,AC和BC相交于点O,OA=OC,OB=OD.求证:AB∥DC.
如图,AC和BC相交于点O,OA=OC,OB=OD.求证:AB∥DC. 如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
如图,直线y=-x+b与反比例函数y=$\frac{k}{x}$的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.