题目内容
9.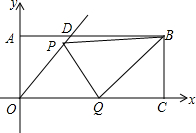 在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.
在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.
分析 设PO的长为x,作PM⊥OQ于M,由矩形的性质和已知条件得出△OPM是等腰直角三角形,得出OM=PM=$\frac{\sqrt{2}}{2}$x,由已知条件得出OQ=$\sqrt{2}$OP=$\sqrt{2}$x,得出MQ=$\frac{\sqrt{2}}{2}$x=OM,因此OP=PQ,证出△BCQ是等腰直角三角形,得出QC=BC=2,求出OQ=OC-CQ=4,得出方程$\sqrt{2}$x=4,解方程即可.
解答 解:设PO的长为x,作PM⊥OQ于M,如图所示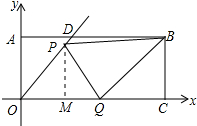 :
:
∵矩形OABC,∠AOC的平分线交AB于点D,
∴△OPM是等腰直角三角形,
∴OM=PM=$\frac{\sqrt{2}}{2}$x,
∵OQ=$\sqrt{2}$OP=$\sqrt{2}$x,
∴MQ=$\frac{\sqrt{2}}{2}$x=OM,
∴OP=PQ,
∴∠PQO=∠POQ=45°,
∵∠PQB=90°,
∴∠BQC=45°,
∴△BCQ是等腰直角三角形,
∴QC=BC=2,
∴OQ=OC-CQ=4,
∴$\sqrt{2}$x=4,
∴x=2$\sqrt{2}$,
即线段PO的长为2$\sqrt{2}$.
点评 本题考查了矩形的性质、坐标与图形性质、等腰直角三角形的判定与性质;熟练掌握矩形的性质,证出等腰直角三角形是解决问题的关键.

练习册系列答案
相关题目
 如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
 如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)
如图,已知AB是⊙O的直径,AD切⊙O于点A,点C是$\widehat{EB}$的中点,则下列结论成立的是①②③(将正确番号填入)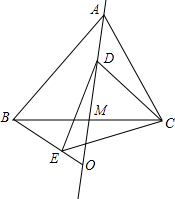 如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.
如图,在等边△ABC中,线段AM为BC边上的中线,动点D在直线AM上时,以CD为一边在CD的下方作等边△CDE,设直线BE与直线AM的交点为O.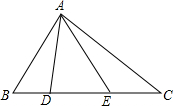 在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.
在△ABC中,AB=14,AE=12,BD=7,BC=28,且∠BAD=∠EAC.