题目内容
20.已知,在四边形ABCD中,AD=BC,E,F,G分别是BD,AB,DC的中点,求证:△EFG是等腰三角形.分析 由于E,F,G分别是BD,AB,DC的中点,利用中位线定理,EF=$\frac{1}{2}$AD,GE=$\frac{1}{2}$BC,又因为AD=BC,所以EF=GE.
解答  证明:∵E,F,G分别是BD,AB,DC的中点,
证明:∵E,F,G分别是BD,AB,DC的中点,
∴EF=$\frac{1}{2}$AD,GE=$\frac{1}{2}$BC.
又∵AD=BC,
∴EF=GE,
即△EFG是等腰三角形.
点评 本题考查了三角形中位线定理和等腰三角形的判定,通过给出的中点,利用中位线定理,证得边相等,从而证明等腰三角形,是一道基础题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
5.若圆锥的底面半径为3cm,展开后所得扇形的半径为4cm,则它的侧面积等于( )
| A. | 12πcm2 | B. | 6πcm2 | C. | 12cm2 | D. | 24πcm |
 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.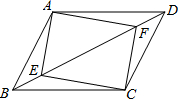 如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.
如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.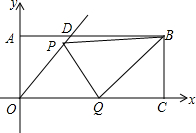 在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.
在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.