题目内容
1. 如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
如图所示,直线y=2x+4与x轴、y轴分别交于A,B两点,以OB为一边在y轴的右侧作等边三角形OBC,将点C向左平移到点C′,且C′恰在AB上,求CC′的长.
分析 过点C作CD⊥x轴于点D,根据点B是直线y=2x+4与y轴的交点求出B点坐标,故可得出OB的长,根据锐角三角函数的定义求出OD及CD的长,故可得出C点坐标,再由点C,C′的纵坐标相同可得出C′E的长,根据CC′=CE+C′E即可得出结论.
解答  解:过点C作CD⊥x轴于点D,
解:过点C作CD⊥x轴于点D,
∵点B是直线y=2x+4与y轴的交点,
∴B(0,4).
∵△OBC是等边三角形,
∴OB=OC=4,∠BOC=60°,
∴∠DOC=30°,
∴CD=$\frac{1}{2}$OC=2,OD=OC•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∴CE=OD=2$\sqrt{3}$.
∵点C,C′的纵坐标相同,
∴2=2x+4,解得x=-1,
∴C′E=1,
∴CC′=CE+C′E=2$\sqrt{3}$+1.
点评 本题考查的是一次函数的图象与几何变换,根据题意作出辅助线,利用直角三角形的性质得出C点坐标是解答此题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
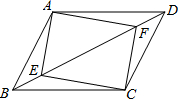 如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.
如图,已知E、F为平行四边形ABCD的对角线上的两点,且BE=DF,∠AEC=90°.求证:四边形AECF为矩形.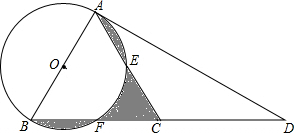 如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F
如图,在△ABC中,AC=BC,延长BC到点D,使CD=CB,连接AD,以AB为直径作⊙O,分别交AC、BC于点E、F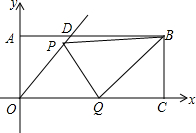 在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.
在平面直角坐标系x、y中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P在线段OD上,点Q线段OC上,OQ=$\sqrt{2}$OP,∠PQB=90°,求线段PO的长.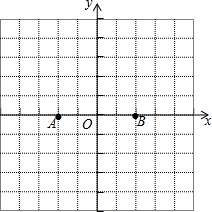 如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).
如图,在平面直角坐标系中,已知点A(-2,0),B(2,0).