题目内容
12.(1)如图1:一个长方形长为2a,宽为2b,若把此图沿图中虚线用剪刀均分为四块小长方形,然后按图2的形状拼成一个大正方形,中间围成一个小正方形(图中阴影部分),请将图2中阴影部分的面积用含a、b的代数式表示出来:(a-b)2,并根据图2面积,写出一个等式:(a+b)2=(a-b)2+4ab(2)如图3,一个长方形长为a,宽为2b,若把此图沿图中虚线用剪刀均分为四块小直角三角形(斜边为c),然后拼成一个正方形,中间围成一个小正方形.
①请画出围成的示意图(按图3所给尺寸大小)
②根据你所画的图形面积写出一个等式,并探究直角三角形三边a、b、c具有怎样的数量关系,用文字语言表述出来.
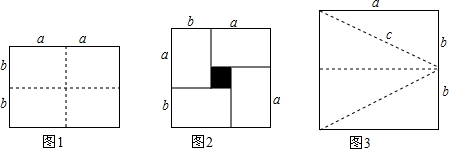
分析 (1)图中阴影部分是边长为a-b的正方形的面积;大正方形的面积等于小正方形的面积加上4个长方形的面积得出等式即可;
(2)①画出的图形是边长为c的正方形;②利用大正方形的面积等于小正方形的面积加上4个长方形的面积得出等式.
解答 解:(1)图2中阴影部分的面积:(a-b)2,
根据图2面积,写出一个等式为:(a+b)2=(a-b)2+4ab;
(2)①如图,
②c2=(a-b)2+4×$\frac{1}{2}$ab,
直角三角形三边a、b、c的关系为a2+b2=c2;
直角三角形中两条直角边的平方和等于斜边的平方.
点评 此题考查图形的剪拼,利用面积之间的关系验证勾股定理,数形结合,解决问题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
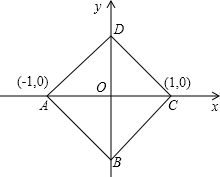 已知如图,点A(-1,0)、C(1,0),以AC为对角线作正方形ABCD.
已知如图,点A(-1,0)、C(1,0),以AC为对角线作正方形ABCD.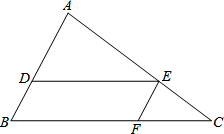 如图,在△ABC中,DE∥BC,EF∥AB.
如图,在△ABC中,DE∥BC,EF∥AB.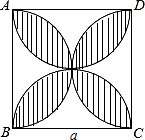 如图,正方形的边长为a,以各边为直径在正方形内画半圆.
如图,正方形的边长为a,以各边为直径在正方形内画半圆. 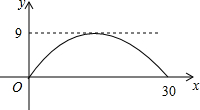 有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.
有一座抛物线形拱桥,其最大高度为9m,现把它的示意图放在如图所示的平面直角坐标系中,则此抛物线的函数解析式为y=-$\frac{1}{25}$(x-15)2+9,其中自变量x的取值范围是0≤x≤30.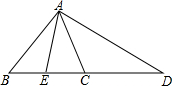 如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.
如图,在△ABC中,E在BC上,D在BC的延长线上,且BE=CE,AD=2AE,AC平∠EAD,求证:CD=AB.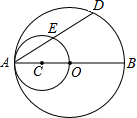 如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.
如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E.