题目内容
7.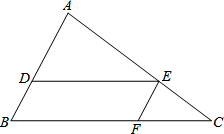 如图,在△ABC中,DE∥BC,EF∥AB.
如图,在△ABC中,DE∥BC,EF∥AB.(1)求证:△ADE∽△EFC;
(2)若AB=7,BC=14,DE:FC=5:2,求四边形BDEF的周长.
分析 (1)根据平行线的性质得到∠AED=∠C,∠EFC=∠B,∠ADE=∠B,等量代换得到∠ADE=∠EFC,于是得到结论;
(2)由DE∥BC,EF∥AB,推出四边形BDEF是平行四边形,根据平行四边形的性质得到DE=BF,BD=EF,由于△ADE∽△EFC,得到$\frac{AD}{EF}$=$\frac{DE}{CF}$=$\frac{5}{2}$,求得$\frac{AD}{BD}$=$\frac{5}{2}$,$\frac{BF}{CF}$=$\frac{5}{2}$,得到BD=2,BF=10,即可得到结果.
解答 解:(1)∵DE∥BC,EF∥AB,
∴∠AED=∠C,∠EFC=∠B,∠ADE=∠B,
∴∠ADE=∠EFC,
∴△ADE∽△EFC;
(2)∵DE∥BC,EF∥AB,
∴四边形BDEF是平行四边形,
∴DE=BF,BD=EF,
∵△ADE∽△EFC,
∴$\frac{AD}{EF}$=$\frac{DE}{CF}$=$\frac{5}{2}$,
∴$\frac{AD}{BD}$=$\frac{5}{2}$,$\frac{BF}{CF}$=$\frac{5}{2}$,
∵AB=7,BC=14,
∴BD=2,BF=10,
∴四边形BDEF的周长=2(2+10)=24.
点评 本题考查了相似三角形的判定和性质,平行四边形的判定和性质,平行线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
2.某文具盒每周的销量与售价的相关信息如下表:
已知该文具盒的进价为6元/个,设售价为x元/个,每周销量为y个.
(1)请直接写出y与x的函数关系式;
(2)设每周的销售利润为W元,求出W与x的函数关系式;
(3)若要使该文具盒的每周利润达到96元,且销量更大,销售单位应定为多少元?
| 售价(元/个) | 10 | 11 | 12 | 13 | … |
| 每周销量(个) | 20 | 18 | 16 | 14 | … |
(1)请直接写出y与x的函数关系式;
(2)设每周的销售利润为W元,求出W与x的函数关系式;
(3)若要使该文具盒的每周利润达到96元,且销量更大,销售单位应定为多少元?
19.若二次函数y=mx2+(m-2)x-1的图象与x轴的交点是A(a,0),B(b,0),且a+b=1,则有( )
| A. | m=-1 | B. | m=1 | C. | m=2 | D. | 无法确定m的值 |
 如图,在△ABC中,∠A=70°,∠ABC=60°,CD平分∠ACB,BE为AC边上的高,求∠BOC的度数.
如图,在△ABC中,∠A=70°,∠ABC=60°,CD平分∠ACB,BE为AC边上的高,求∠BOC的度数.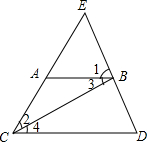 如图,下列推理所注的依据正确的是(3)(填序号)
如图,下列推理所注的依据正确的是(3)(填序号)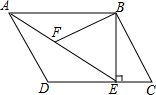 如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE.F为AE上一点,且∠BFE=∠C.