题目内容

20．抛物线y=2x2-5x+1与x轴的公共点的个数是两个．

分析 抛物线与x的交点个数，即为抛物线y=2x2-5x+1与x轴的公共点的个数，因此只要算出b2-4ac的值就可以判断出与x轴的交点个数．

解答 解：∵y=2x2-5x+1，
∴b2-4ac=（-5）2-4×2×1=17＞0．
∴抛物线y=2x2-5x+1与x轴有两个交点．
即：抛物线y=2x2-5x+1与x轴的公共点的个数是两个．
故答案为：两个．

点评 本题考查二次函数与x轴的交点问题，关键是算出二次函数中b2-4ac的值．

练习册系列答案
相关题目
10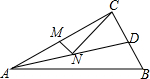．如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm，AD平分∠CAB交BC于点D，点M，N分别是AC和AD边上的动点，则MN+NC的最小值为（　　）
A．$\frac{3}{2}$B．2C．$\frac{5}{2}$D．$\frac{12}{5}$
11．数轴上离开原点3$\frac{1}{2}$个单位长度的点所表示的数是3$\frac{1}{2}$或-3$\frac{1}{2}$．
8．观察下列等式：（x-1）（x+1）=x2-1，（x-1）（x2+x+1）=x3-1，（x-1）（x3+x2+x+1）=x4-1
（1）请你猜想一般规律：（x-1）（xn-1+xn-2+…+x2+x+1）=xn-1；
（2）已知x4+x3+x2+x+1=0，分别求x5-1及x2010的值．
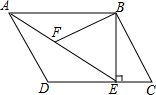15．如图，在平行四边形ABCD中，过点B作BE⊥CD，垂足为E，连结AE．F为AE上一点，且∠BFE=∠C．
（1）求证：△ABF∽△EAD；
（2）若AB=4，BE=3，AD=$\frac{7}{2}$，求BF的长．
5．下列说法正确的有（　　）
①无限小数都是无理数；       ②带根号的数都是无理数；
③有限小数都是有理数；        ④实数与数轴上的点是一一对应的．
A．3个B．2个C．1个D．0个
12．（1）如图1：一个长方形长为2a，宽为2b，若把此图沿图中虚线用剪刀均分为四块小长方形，然后按图2的形状拼成一个大正方形，中间围成一个小正方形（图中阴影部分），请将图2中阴影部分的面积用含a、b的代数式表示出来：（a-b）2，并根据图2面积，写出一个等式：（a+b）2=（a-b）2+4ab
（2）如图3，一个长方形长为a，宽为2b，若把此图沿图中虚线用剪刀均分为四块小直角三角形（斜边为c），然后拼成一个正方形，中间围成一个小正方形．
①请画出围成的示意图（按图3所给尺寸大小）
②根据你所画的图形面积写出一个等式，并探究直角三角形三边a、b、c具有怎样的数量关系，用文字语言表述出来．
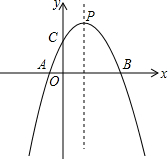9．如图，抛物线y=-x2+bx+c的对称轴是直线x=1，与y轴交于点C（0，3），与x轴交于 A，B两点．
（1）请写出这个抛物线的解析式；
（2）若此抛物线与x轴交于A，B两点，顶点是P，求△ABP的面积．
参考公式：顶点坐标（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$）
10．计算．
（1）7-（-2）+（-3）．
（2）$（-\frac{3}{7}）+\frac{5}{6}-（-2\frac{1}{7}）+（-\frac{5}{6}）$
（3）$16÷{（-2）^3}-\frac{1}{6}×（-3）$
（4）（-81）÷$\frac{9}{4}×\frac{4}{9}$÷（-16）
（5）（$\frac{1}{2}-\frac{5}{9}+\frac{7}{12}$）×（-36）
（6）$1\frac{1}{2}$×$\frac{5}{7}-（-\frac{5}{7}）$×$2\frac{1}{2}$+（-$\frac{1}{2}$）$÷1\frac{2}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网